One of the foundations of computer science today is data. The omnipresence of increasingly large volumes of data has become a key driver for many innovations and new research directions in computer science. Specifically in information systems, data – and the analytics developed on top of this data – have transformed the field from expert-driven to evidence-based, which in turn massively broadens the applicability of results to more and larger contexts. Our main mission is to bridge the gap between process science (BPM, WFM, formal methods, etc.) and data science. This explains the focus on process mining.

Research
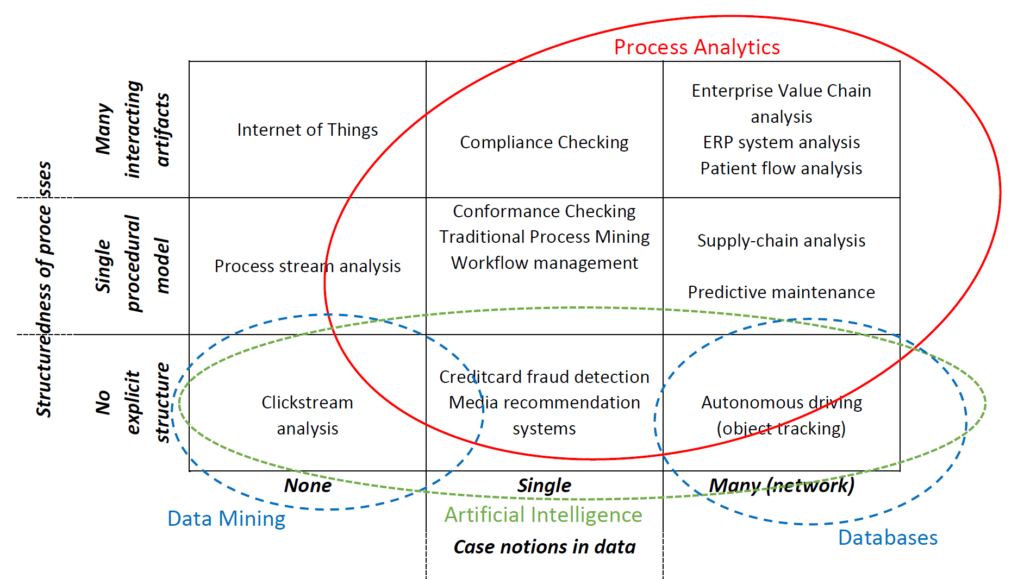
The process analytics group focusses on the interplay between processes, the data these processes generate, the models that are used to describe them, and the systems that support these processes. The group distinguishes itself in the Information Systems discipline by its fundamental focus on modelling, understanding, analyzing, and improving these processes. Essentially, every time two or more activities are performed to reach a certain goal, fundamental principles of processes apply. Processes take place on the level of individual actors, groups of actors, entire organizations, and networks of organizations and they can be structured explicitly or implicitly through networks of interacting artifacts.
Articles authored by all members of the group are internationally known for their strong theoretical foundation, extensive validation, and real-life case studies.
Education
This is further reflected in the teaching done by the group, starting in the Bachelor with the university-wide base course on Data Analytics to advanced Master level courses on Process Mining. As a responsible group for many data challenges the link between real-world applications and scientific advances is always tight.
Through our interest in real-life, hard problems, we have set up various collaborations with industrial and societal partners. By making real-life data publicly available (with permission of the data owners) the group sets the benchmarks for researchers worldwide. The data have been published in the 4TU.Centre for Research Data since 2010 and our datasets are consistently among the most popular downloads since.
Tool Development
The extensive validations that are delivered by our group are made possible by the infrastructure which we built over the past 15 years. A main role is played by the process mining framework ProM (process mining and process analysis), which serves as a benchmark for rapid prototyping in process analysis research worldwide. Furthermore, the modelling tool CPNide, which is essential for our courses and experimentation, receives continued support from our group.
Staff
The group consists of several fulltime researchers, lecturers and PhD students.
