Welcome to WHIZZKIDS '96

On this website you will find information about the Whizzkids '96 Contest. This mathematics challenge has been sponsored by CMG (consultants in information technology) and was published by De Telegraaf (a Dutch newspaper). The problem to be solved has been designed by Jan Karel Lenstra (EUT/CWI), Emile Aarts (EUT/Philips Research) and co-workers.

Competition was open for everybody, and there was a special category for professionals (i.e., those who are involved in mathematics and computing science research and teaching).

The problem

A complete Dutch description was available, at the time of publication of the puzzle, at CMG. The problem is to cluster and route a news paper delivery plan. Four news paper delivery boys deliver 120 newspapers to the subscribers. They start at the same time from a single depot. The problem is to deliver the LAST newspaper AS EARLY AS POSSIBLE. To avoid numerical difficulties the problem has been situated in Manhattan. Therefore we can describe the subscribers' addresses by simple (x,y)-coordinates, and the distance between any pair of subscribers is defined by the Manhattan-distance. A numerical table is obtained from the numerical data file.

Solutions

We received over 900 submissions. In some of these some mistakes were made, in particular in computing the distances. However most people had no problem in describing a feasible solution. A 14 year old high school student using a paper-and-pencil approach even beat the professional participants!!! The best solution was found by a group of Eindhoven students in Computing Science. The last news paper is delivered at 1183 time units from the start. There were more solutions with this value, but the Eindhoven students had also the smallest average delivery time. Find hereunder their story of sleepless nights. A solution similar to the one found by the students is given in the following figure.

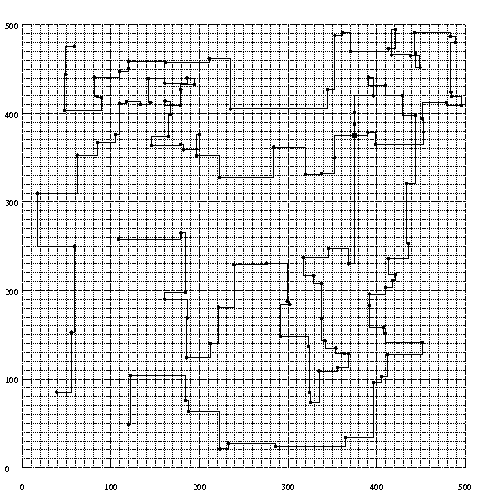
with the four routes given by:

0 83 84 89 86 96 104 109 105 106 98 102 101 95 88 87 93 94 112 97 92 90 79 56 51 49 42 37 21 18

0 73 69 61 55 50 44 45 36 34 25 30 31 27 32 35 43 41 28 23 24 22 17 15 13 10 8 1 6 5 2

0 81 72 60 65 68 67 70 75 78 80 76 66 64 63 62 57 59 58 54 53 48 47 39 40 26 38 33 14

0 85 91 114 113 115 120 118 117 119 116 108 110 111 107 100 103 99 82 77 74 71 52 46 29 20 19 16 9 11 12 3 4 7

Note that this is not necessarily the optimum solution. We can prove a lower bound of 1160, so a gap remains of 2 percent. The professionals did not do too well in 1996. Of course students can spend much more time and computing power on these real-life instances of combinatorial problems...

It is also possible to use a computer as a tool for supporting a solution approach based on human insight. Diego Lont (also an Eindhoven Computing Science student) together with his colleagues designed a tool that displays the routes on a screen, and allows the user to modify the routes by moving addresses between the routes. Solution characteristics are automatically updated. It is found in route editor file.

We hope that everyone has enjoyed this puzzle. There is still one open question, with a reward: The first one to produce a solution with a maxiaml routelength STRICTLY LESS than 1183, OR with a MATHEMATHICALLY SOUND PROOF that no such solution exists, can win another 5000 GUILDERS from CMG.

Update: it has been shown by Bill Cook et al that the best solution submitted is the true optimum solution, both for a min-max of 1183, as well as the minimum average delivery time 558.81667. A full description is found in David Applegate, William Cook, Sanjeeb Dash, André Rohe, (2002) Solution of a Min-Max Vehicle Routing Problem. INFORMS Journal on Computing 14(2):132-143. Online version.

This page was modified last on: December 23, 1997,
by Cor Hurkens (wscor@win.tue.nl)