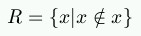
This is a good definition. However, one would like to have a concept "cardinality" (rather than "the same cardinality"), so that one can talk about the cardinality of a set.
The first proposal was: a cardinality is an equivalence class for the equivalence relation "having the same cardinality".
Is it an element of itself? The answer is neither yes nor no, and this shows that mathematics does not remain consistent when it is allowed to define sets by arbitrary properties.
Russell's solution was to introduce a hierarchy of types, so that a set whose elements are of some type itself has a higher type. That it is possible to set up all of mathematics in this way, starting from logic only, was shown in the famous treatise Principia Mathematica by Russell & Whitehead.
A practical setup for mathematics, following the work of Zermelo-Fraenkel-Bernays-Gödel-von Neumann, is the following two-level system.
One has sets and classes. Every property defines a class. A set is a class, but not every class is a set. The elements of a class are sets. Two classes with the same elements are equal.
In this formalism one may write down the above definition of R, and see that it defines a class. If R is a set then a contradiction is obtained, so R is a class that is not a set, a proper class.
(i) the empty set is a set,
(ii) given two sets x, y, the class {x,y} that has only them as elements is a set,
(iii) given a set x, the union of its elements is again a set,
(iv) given a set x and a class A and a function f mapping x into A, the image f[x] of x under f is a set,
(v) given a set x and a class A, the intersection of x and A is a set,
(vi) the power set of a set is a set,
(vii) "Foundation": every nonempty set x has an element that is
disjoint from it.
[This makes sure e.g. that one cannot have x = {x}.]
(viii) "Infinity": there exists an infinite set.
[More concretely, perhaps: there exists a set ω that has the empty
set as an element, and if a is an element of ω, then also
the union of a and {a} is an element of ω.]
(ix) "Axiom of choice": if x is a set such that its elements are pairwise disjoint and nonempty, then there exists a set s that contains precisely one element from each element of x.
An ordinal number is a set that is well-ordered by the relation "is element of".
Thus, we have ordinal numbers
The existence of the set ω0 is guaranteed by the axiom of infinity.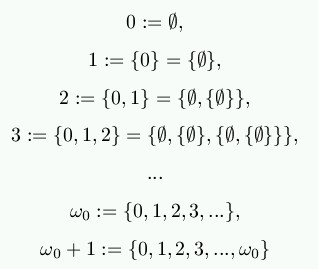
Theorem [Burali-Forte paradox]
The class On of ordinal numbers is well-ordered by
"is-element-of". Consequently, it is not a set.
Theorem Every set can be well-ordered.
If we accept that, then given a set we find a bijection between that set and some ordinal number. (By transfinite construction we find a bijection between the set and some initial segment of On. It cannot be all of On, for then On would be a set by Axiom (iv), contradicting Burali-Forte.)
Two ordinal numbers may have the same cardinality. For example, lots of ordinals are countable. Define a cardinal number as an ordinal number that does not have the same cardinality as any smaller one.
In this way we get "cardinality" as a number, namely, a cardinal number, rather than the vague "equivalence class of all things of the same cardinality".
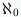(aleph null or aleph nought)
is the first infinite cardinal, the cardinality of the set of integers.
Addition and multiplication of infinite cardinals is rather boring: the sum of two infinite cardinals (defined as the cardinality of the disjoint union) equals the largest of them, and the same holds for the product (defined as the cardinality of the cartesian product). First exponentiation becomes interesting.
It is an easy exercise to show that the power set of X has a larger cardinality than X, for any set X. Thus,
One defines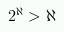
for the cardinality of the set of real numbers.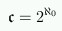
The Continuum Hypothesis says that c equals
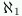(aleph one),
the smallest uncountable cardinal.
It is consistent to assume this [Gödel], but also consistent
to assume that the set of reals is much larger [Cohen].
Exercise Prove
The open sets in the plane are unions of the (countably many) open balls with rational radius and rational center, so there are c of them, and hence there are also c closed sets. Well-order the set of closed sets, where the ordinal of this well-ordering is the smallest possible, i.e., c. For each closed set C of cardinality c, pick two points aC and bC, never chosen before. ("Before": for some earlier closed set.) This is possible since any initial segment of the row of closed sets has cardinality smaller than c, so we have not yet used all points of C. Now let A be the set of all points aC. The pathcomponents of this set are single points, since a path C not reduced to a point is a closed set of cardinality c, but bC is not in A, so A does not contain the path C. On the other hand, A is connected, for otherwise there would be a curve or line C disjoint from A separating the plane, with parts of A on both sides, but C contains aC so is not disjoint from A.
