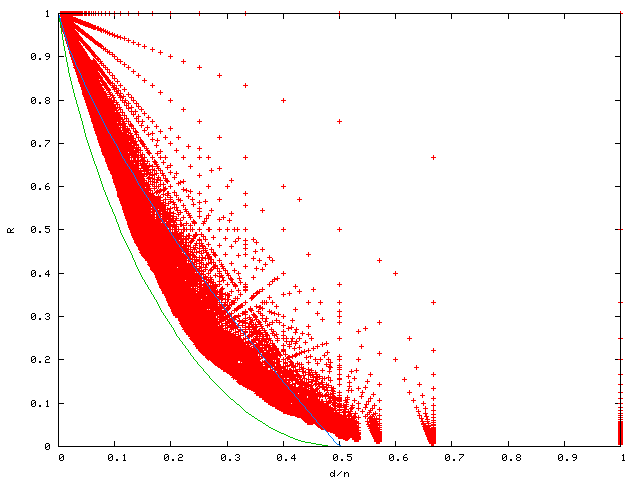
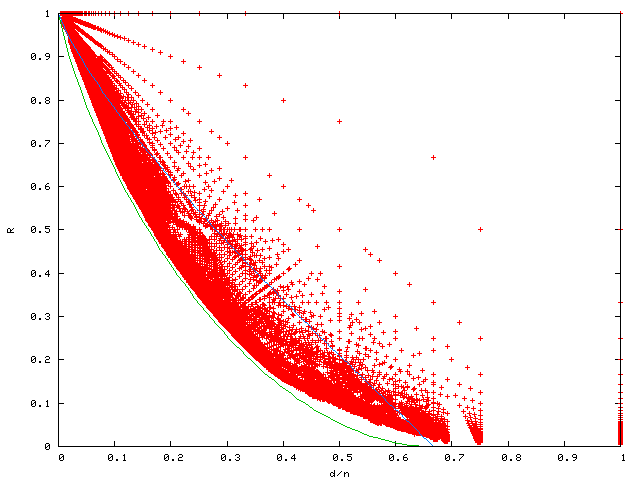
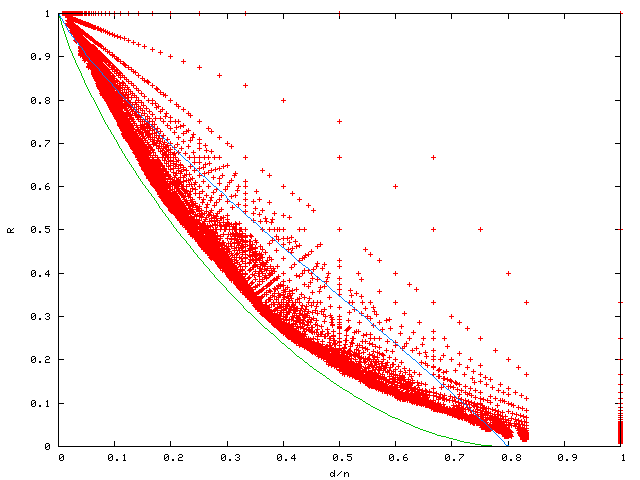
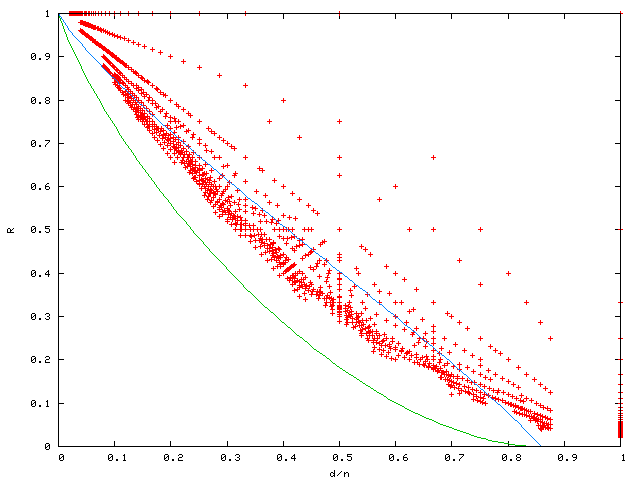
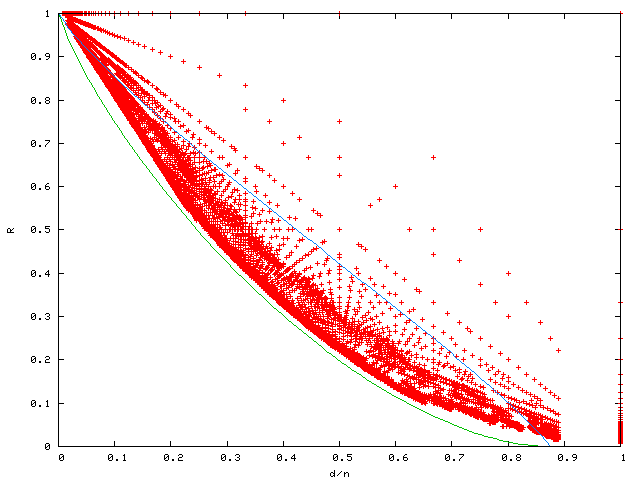
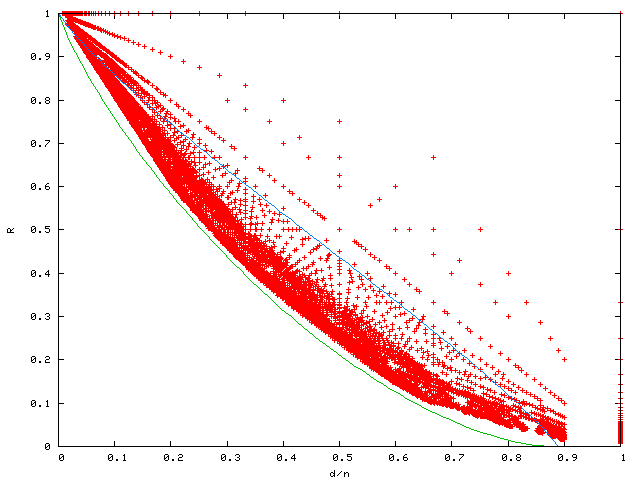
Trivial codes have k=n and d=1, or d=n and k=1.
The green line is the Gilbert-Varshamov asymptotic lower bound. We are guaranteed the existence of arbitrarily long codes above this bound.
The blue line is the Elias asymptotic upper bound: in the limit (with code length tending to infinity) codes with positive rate must remain below this. Other asymptotic bounds, such as the McEliece-Rodemich-Rumsey-Welch bound, are still slightly smaller.