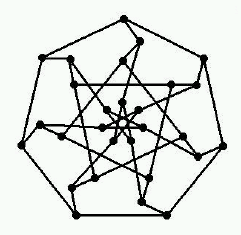
There is a unique distance-regular graph with intersection array {3,2,2,1;1,1,1,2}. It has 28 vertices and spectrum 31 28 (√2 – 1)6 (–1)7 (–√2 – 1)6. This is the graph that Coxeter calls "My graph".
Equivalently, this is the graph on the antiflags of the Fano plane, where (P,L) is adjacent to (Q,M) when P,Q are not on L,M.
a) partition into three 7-gons and a 7-coclique There are 8 of these, forming a single orbit. The stabilizer of one is 7:6, with vertex orbit sizes 7+21. (There are 24 heptagons. The set of 7 neighbours of a heptagon is a 7-coclique corresponding to a Fano plane. There are 8 such Fano 7-cocliques, each adjacent to three heptagons.)
b) A 4-set, all mutual distances 4. There are 14 of these, forming a single orbit. The stabilizer of one is S4, with vertex orbit sizes 4+12+12. These correspond to the antiflags containing a given point or a given line. The graph on these 4-sets, adjacent when they have nonempty intersection, is the Heawood graph.
c) A pair of edges at distance 4. There are 21 of these, forming a single orbit. The stabilizer of one is D16, with vertex orbit sizes 4+8+8+8. These correspond to the flags of the Fano plane.
d) A vertex. There are 28 of these, forming a single orbit. The stabilizer of one is D12, with vertex orbit sizes 1+3+6+12+6. These correspond to the antiflags of the Fano plane.
The girth is 7. The binary code generated by the cycles has parameters [42,15,7], with weight enumerator
0: 1 7: 24 8: 21 9: 56 10: 84 12: 140 13: 336 14: 528 15: 896 16: 987 17: 1344 18: 2296 19: 3024 20: 3360 21: 3760 22: 4368 23: 4200 24: 3087 25: 2184 26: 1428 27: 560 28: 84Thus, there are 24 7-gons and 21 8-gons and no 11-gons. The 84 words of weight 28 are disjoint unions of two 14-gons - their complements are the 84 complete matchings. In particular, the Coxeter graph is 3-edge-colorable. (By Brooks' theorem it is also 3-colorable.)
H.S.M. Coxeter, My graph, Proc. London Math. Soc. 46 (1983) 117-136.
[BCN], Section 12.3.