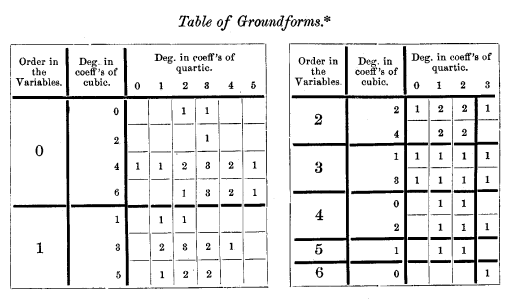
In the particular case of V4+V3 Gundelfinger found 64 generators for the algebra of covariants. Sylvester thought that the minimal number is 61 and wrote three papers on this question. It is 63. This settles a 141-year old problem.
Sigmund Gundelfinger, Zur Theorie des simultanen Systems einer cubischen und einer biquadratischen binären Form, Habil.schr., J. B. Metzler, Stuttgart, 1869. PDF
J. J. Sylvester, Sur les covariants fondamentaux d'un système cubo-biquadratique binaire, Comptes Rendus 87 (1878) 242-244, 287-289. scan
J. J. Sylvester, Sur le vrai nombre des formes irréductibles du système cubo-biquadratique Comptes Rendus 87 (1878) 445-448. scan
J. J. Sylvester, Détermination du nombre exact des covariants irréductibles du système cubo-biquadratique binaire, Comptes Rendus 87 (1878) 477-481. scan
J. J. Sylvester & F. Franklin, Tables of the generating functions and groundforms for simultaneous binary quantics of the first four orders, taken two and two together, Amer. J. Math. 2 (1879) 293-306.
J. H. Grace & A. Young, The algebra of invariants, Cambridge, 1903.
A. E. Brouwer & M. Popoviciu, Sylvester versus Gundelfinger, SIGMA 8 (2012), 075.
1 + t2 + t3 + 2t4 + 3t5 + 5t6 + 7t7 + 11t8 + 16t9 + 22t10 + 30t11 + 42t12 + 55t13 + 73t14 + 95t15 + 121t16 + 153t17 + 193t18 + 238t19 + 294t20 + ...
Again, but now in multidegrees: ∑ aij ti uj, where aij is the dimension of the space of invariants of degree i in the coefficients of V4 and of degree j in the coefficients of V3:
1 + t2 + t3 + t4 + u4 + t5 + t3u2 + tu4 + 2t6 + 3t2u4 + t7 + t5u2 + 5t3u4 + 2t8 + t6u2 + 6t4u4 + t2u6 + u8 + 2t9 + t7u2 + 8t5u4 + 4t3u6 + tu8 + 2t10 + t8u2 + 11t6u4 + 4t4u6 + 4t2u8 + ...
Poincaré series for the covariants (∑ aijk ti uj vk, where aijk is the dimension of the space of covariants of degree i in the coefficients of V4 and of degree j in the coefficients of V3 and of degree k in the variables x):
1 + t2 + t3 + tuv + t4 + u4 + t2uv + u2v2 + uv3 + t5 + t3u2 + tu4 + t3uv + 2tu3v + 2tu2v2 + tuv3 + tv4 + 2t6 + 3t2u4 + 2t4uv + 3t2u3v + 4t2u2v2 + 2t2uv3 + u3v3 + t2v4 + t7 + t5u2 + 5t3u4 + 2t5uv + 4t3u3v + 2tu5v + 5t3u2v2 + 2tu4v2 + 3t3uv3 + 2tu3v3 + t3v4 + 2tu2v4 + tuv5 + 2t8 + t6u2 + 6t4u4 + t2u6 + u8 + 2t6uv + 7t4u3v + 4t2u5v + 7t4u2v2 + 4t2u4v2 + u6v2 + 3t4uv3 + 5t2u3v3 + u5v3 + 2t4v4 + 3t2u2v4 + u4v4 + 2t2uv5 + u3v5 + u2v6 + 2t9 + t7u2 + 8t5u4 + 4t3u6 + tu8 + 3t7uv + 8t5u3v + 7t3u5v + 2tu7v + 8t5u2v2 + 8t3u4v2 + 3tu6v2 + 4t5uv3 + 9t3u3v3 + 3tu5v3 + 2t5v4 + 5t3u2v4 + 4tu4v4 + 3t3uv5 + 3tu3v5 + t3v6 + 2tu2v6 + tuv7 + 2t10 + t8u2 + 11t6u4 + 4t4u6 + 4t2u8 + 3t8uv + 9t6u3v + 12t4u5v + 5t2u7v + 10t6u2v2 + 11t4u4v2 + 8t2u6v2 + 5t6uv3 + 11t4u3v3 + 8t2u5v3 + u7v3 + 2t6v4 + 7t4u2v4 + 9t2u4v4 + 4t4uv5 + 7t2u3v5 + u5v5 + 5t2u2v6 + u4v6 + 2t2uv7 + t2v8 + ...
| d\o | 0 | 1 | 2 | 3 | 4 | 5 | 6 | # | cum |
|---|---|---|---|---|---|---|---|---|---|
| 1 | - | - | - | 1 | 1 | - | - | 2 | 2 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | - | 6 | 8 |
| 3 | 1 | 1 | 2 | 2 | 1 | 1 | 1 | 9 | 17 |
| 4 | 1 | 2 | 2 | 2 | 1 | - | - | 8 | 25 |
| 5 | 2 | 3 | 3 | 1 | 1 | - | - | 10 | 35 |
| 6 | 2 | 3 | 2 | 1 | - | - | - | 8 | 43 |
| 7 | 3 | 3 | 1 | - | - | - | - | 7 | 50 |
| 8 | 3 | 2 | - | - | - | - | - | 5 | 55 |
| 9 | 4 | 1 | - | - | - | - | - | 5 | 60 |
| 10 | 2 | - | - | - | - | - | - | 2 | 62 |
| 11 | 1 | - | - | - | - | - | - | 1 | 63 |
This table was produced by generating basic transvections for V4+V3. Next checked by producing invariants for V4+V3+V1 up to degree 29. This suffices, as follows from the existence of a homogeneous system of parameters with degrees 3,4,4,5,5,6,6,7 (joint work with M. Popoviciu).
Sylvester & Franklin gave the following table:

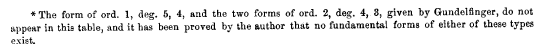
with 61 forms (degorders (9,1) and (7,2) are missing). Apparently, Gundelfinger did have our 63 forms, together with one superfluous form. Grace & Young write (p. 131-132):


In reality, of course, the case of the septimic was settled only later.
In the second paper he observes that it follows from the Poincaré series that there are 8 linearly independent covariants of multidegree (3,4,2). Next, he constructs 8 reducible such covariants (products of covariants of lower degree) and argues that these are linearly independent. However, the forms are dependent and only seven are independent. (The easiest way to see that, if one computes modulo a small prime where the dependence might have been introduced by the modular reduction, is to produce the eighth covariant. Take c, the cubic, and f, the quartic, and form f204 = (f,f)2, f306 = (f,f204)1, f313 = (c,f306)3, f324 = (c,f313)1, f331 = (c,f324)3, f342 = (c,f331)1. Then f342 is independent of the products of covariants of smaller degree.) Then:

In the third paper he observes that it follows from the Poincaré series that there are 12 linearly independent covariants of multidegree (4,5,1). Next, he constructs 12 reducible such covariants and argues that these are linearly independent. However, the forms are dependent and only eleven are independent. (The twelfth invariant can be produced as follows: form f113 = (c,f)2, f451 = (c,f113f331)3. Then f451 is independent of the products of covariants of smaller degree.)

(False theorem omitted.)
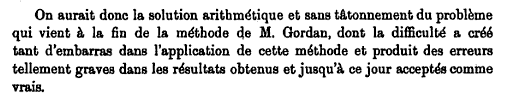
Die kurz zugemessene Zeit gestattete nur noch, in §8 ein solches volles System ohne Beweis anzugeben, wie es sich Herrn Professor Gordan als specielle Anwendung einer allgemeinen Theorie darbot und wie es mir von Herrn Professor Clebsch schriftlich mitgetheilt worden. ...He deems Gordan's notation obscure:
Es wird in diesem Paragraphen zunächst das volle System aufgestellt werden, wie es bei Prof. Gordan's Bezeichnung sich gestaltet, und wie es mir Prof. Clebsch mitgetheilt hat. Aus dieser denn noch sehr schattenhaften* Darstellungsart wird dann dasselbe in die gewöhnliche symbolische Ausdrucksweise übertragen und mit den bereits betrachteten Formen verglichen. ...*) Selbstverständlich soll die Benennung "schattenhaft" keinen Vorwurf für Gordan's Bezeichnungsweise enthalten; wir glauben im Gegentheil, dass mit derselben und mit den sich ihr anschliessenden Methoden eine neue Aera in der modernen Algebra hereinbricht, beziehungsweise schon hereingebrochen ist.