Singular structures in variational pdes
Amsterdam, July 14th-18th, 2008
NB Maria Westdickenberg and Piotr Gwiazda have cancelled, unfortunately. Mark Peletier and Matthias Röger will give a talk instead.
Singular structures appear in a a variety of applications and pose an interesting challenge for a mathematical analysis. Variational methods have proved a valuable tool to understand fundamental features of the models. The identification of microstructures in material sciences, the evolution of damages in mechanics, stochastically perturbed models in phase transition theory, or pattern formation in block copolymers are examples of the topics that we are interested in. Variational structures provide strong entry points into the understanding of such complex phenomena, by allowing the use of techniques such as energy minimization, gradient flows, and Gamma-convergence.
The mini-symposium is scheduled during 5ECM on Friday July, 18th, in two slots: 10.30-12.00 and 13.30-15.00, separated by lunch. There will be six talks of 30 minutes each.
Matthias Röger (MPI Leipzig): Convergence of an Allen-Cahn equation to forced mean curvature flowPhase field models are a common approach to phase separation processes. They are often given as gradient flows of a diffuse surface energy that goes back to van der Waals and Cahn-Hilliard. Often these models correspond formally to a sharp interface limit. To justify the passage to the limit techniques from geometric measure theory have proved useful. As a particular example we consider the convergence of a perturbed Allen-Cahn equation to a forced mean curvature flow.
Matthias Kurzke (Institute for Applied Mathematics, University of Bonn, Germany): Vortices in Chern-Simons Higgs theories away from self-duality (joint work with Daniel Spirn)
Abelian Chern-Simons Higgs theory is a classical field theory
on (2+1)-dimensional Minkowski space. We study the energy
functional governing static solutions,
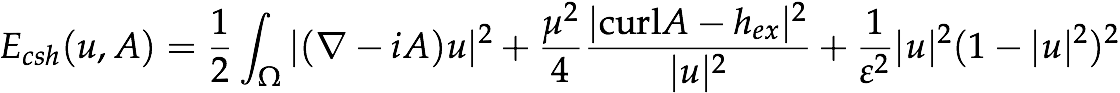
with a Γ-convergence approach
that allows us to drop the usual assumption μ = ε
of self-duality.
Our results are based on a compactness result for Jacobians
that extends previous results for the Ginzburg-Landau functional.
We are able to show compactness for
Jacobians of u under bounds on the energy
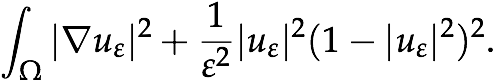
As applications we study how topological vortices can be induced by
an external magnetic field and determine the behavior of
energy minimizers in various scalings.
Xiaofeng Ren (George Washington University, Washington): On the resonance condition of a singular limit problem from the Ohta-Kawasaki and the Gierer-Meinhardt theories
The resonance condition, also known as the gap condition, has appeared in several recently studied singular perturbation problems. One natural question is whether such a condition is superfluous, and a better question is whether the condition implies a bifurcation phenomenon. In this talk I will discuss this condition in the case of a geometric problem that arises as a singular limit of the Ohta-Kawasaki theory of block copolymers and also of the Gierer-Meinhardt theory of morphogenesis. We show that in general standard bifurcation does not occur and the cause of resonance is typically an imperfect type of bifurcation.
Marc-Oliver Rieger (Zürich): Two applications of transport theory: gradient flows of Young measures and portfolio optimization
In the first part of my talk I present results on gradient flows of Young measures in the context of damage in a material. We model the deformation gradient by a Young measure and assume a quasi-static evolution of this Young measure in a non-convex and non-coercive energy of Lennard-Jones type. The main feature of this approach is that it allows for local, rather than global minimization of deformations and can thus model hysteresis. The goal is to find a unified model that covers elastic behavior, damage and fracture. This is joint work with Johannes Zimmer (University of Bath). A fundamental ingredient of this model are results from transport theory. These results have another interesting application in a very different field, namely in financial mathematics or more precisely in portfolio optimization. In the second part of my talk I will explain this connection and prove that under very weak conditions optimal financial products on complete markets have to be co-monotone with the inverted state price density. In the special case of a market described by the Capital Asset Pricing Model this implies that the payoff of an optimal financial product can be written essentially as a function of the market portfolio and is monotone. This result can be used to derive existence and non-existence results for optimal financial products.
Didier Smets (Laboratoire Jacques-Louis Lions, Paris VI): Stability of the kink for the NLS flow
We will discuss travelling wave solutions to the Gross-Pitaevskii equation in dimension 1, 2 and 3. In 1D, a special example is given by the well-known kink, or black soliton, v_0(x) = tanh(x/√2), which is actually stationary. The kink has long been known to be stable for the dissipative evolution flow, which in this case is the Allen-Cahn equation. In a joint work with F. Bethuel, P. Gravejat and J.-C. Saut, we prove that it is orbitally stable for the Hamiltonian flow.
Mark Peletier (Technische Universiteit Eindhoven): Many-spike structures in block copolymers
Block copolymers owe their technological importance to their ability to form structures with a wide variety of patterns. The simplest form is a diblock copolymer, which consists of two subpolymers (A and B 'blocks') grafted together. If the two blocks repel each other, phase separation ensues, causing A-rich and B-rich regions to appear. At the same time, the chemical bond between the two parts limits the spatial scale of separation, giving rise to many different patterns, all with a well-defined length scale.
Most of these patterns are all but inaccessible by analytical means. In a limit of highly skewed mass distribution, however, we show that structures appear for which the limiting energy can be represented in a simple form. These structures consist of many concentrated, near-spherical regions of one phase in a sea of the other phase.
The energy for these structures is dominated by a single-spike term, which penalizes each spike independently. This term drives the system towards spikes of a well-defined size. At the next level the interaction between the spikes is given by a Coulomb interaction potential, giving rise to approximately periodic arrangements.
Organizers: Matthias Röger (MPI Leipzig) and Mark Peletier (Eindhoven)