
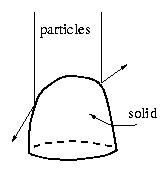
 Imagine you're designing the nose of a high-speed train. Main design
goal: to minimize air resistance. Although he wasn't thinking
of trains, Sir Isaac Newton formulated this problem in his
Principia Mathematica, first published in 1687. He modelled
the problem by assuming that every air particle hit the body
(the nose of the train) exactly once. In the collision between body
and particle momentum is passed from the particle to the body,
and the amount of momentum depends on the angle that the surface of
the body makes at that point with the direction of the particle,
as shown in the figure. The total resistance then is the sum
over the body of this transfer of momentum.
Imagine you're designing the nose of a high-speed train. Main design
goal: to minimize air resistance. Although he wasn't thinking
of trains, Sir Isaac Newton formulated this problem in his
Principia Mathematica, first published in 1687. He modelled
the problem by assuming that every air particle hit the body
(the nose of the train) exactly once. In the collision between body
and particle momentum is passed from the particle to the body,
and the amount of momentum depends on the angle that the surface of
the body makes at that point with the direction of the particle,
as shown in the figure. The total resistance then is the sum
over the body of this transfer of momentum.
If we describe the surface of the body as the graph of a function u, then we can state the problem in mathematical terms in the following way:

Newton himself provided a solution to this minimization problem in the case where Omega is a ball in R², limiting himself to functions that have radial symmetry. This reduces the 2-D integral to a one-dimensional one and greatly simplifies the analysis. Here are some pictures of the solution that he found:
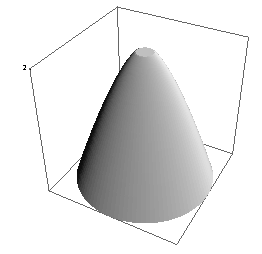
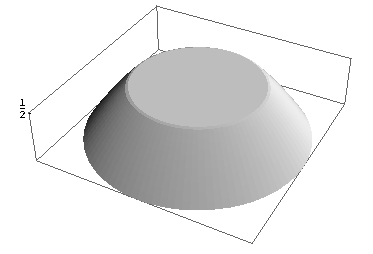
The left picture is for M = 2, the right picture for M = 0.5. In both cases the radius of the ball is 1. (Thanks to Paolo Guasoni for the pictures). Although it is counterintuitive, the solution provided by Newton contains a flat zone at height M which varies in size (depending on M) but is always present.
Newton's formula for the air resistance (the integral in (1)) is found in many engineering handbooks, and his solution is presented as a simple application of the calculus of variations. Throughout the three hundred years that have passed since the first publication of the Principia, no-one seemd to ask a very simple and obvious question: if Omega is a ball, is the minimizer necessarily radially symmetric? In other words, does the solution copy the symmetry of the domain? And was Newton therefore justified in assuming that the minimizer is radially symmetric?
Intuition tells us that this is true, as does a comparison with many other minimization problems. But it is false, in fact: in 1996 a paper was published by F. Brock, V. Ferone, and B. Kawohl, where it was proved that the minimizer on the ball is not radially symmetric. This was done by showing that the minimizer could not be at the same time both strictly concave and smooth. Since Newton's solution has both these properties - apart from the top flat zone - this shows that this function does not minimize among all functions. Since it does minimize among radially symmetric functions, the `real' minimizer must be non-radially symmetric.
This result opened the witch-hunt for the answer of the immediate question:
We managed to prove a couple of things, though.
T. Lachand-Robert and Mark A. Peletier, An Example of Non-convex Minimization and an Application to Newton's Problem of the Body of Least Resistance, Annales de l'Institut Henri Poincaré, Analyse non linéaire 18, pp. 179-198 (2001)
If u is the minimizer of Newton's problem, then for any open subet of Omega, u is not strictly convex on that subset.Or, said differently, the graph of u must contain a dense set of straight line segments.
I called this result a generalization, but I mean to stress that the proof is not a simple extension of the proof given by Brock et al. Because of the lack of regularity, choosing an appropriate class of perturbations of the minimizer is highly non-trivial, since most perturbations make the function non-concave and therefore take it outside of the set of admissible functions.
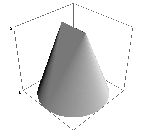 The fact that u (the minimizer) is non-strictly
concave does not give a lot information about its actual form, however.
Whilst trying to imagine possible forms, it might be useful to think of
the function here on the right, discovered by Guasoni
(he called it the screwdriver). For large values of M (M >= 2)
the screwdriver has a lower resistance than Newton's function. Note that
the screwdriver is indeed non-strictly concave, everywhere: from
every point on the circular base there runs at least one straight
line up to the top.
The fact that u (the minimizer) is non-strictly
concave does not give a lot information about its actual form, however.
Whilst trying to imagine possible forms, it might be useful to think of
the function here on the right, discovered by Guasoni
(he called it the screwdriver). For large values of M (M >= 2)
the screwdriver has a lower resistance than Newton's function. Note that
the screwdriver is indeed non-strictly concave, everywhere: from
every point on the circular base there runs at least one straight
line up to the top.
T. Lachand-Robert and Mark A. Peletier, Newton's Problem of the Body of Minimal Resistance in the Class of Convex Developable Functions (930 kB), Mathematische Nachrichten, Vol. 226, pp. 153-176 (2001).




T. Lachand-Robert and Mark A. Peletier, Extremal Points of a Functional on the Set of Convex Functions, Proceedings of the AMS, Vol. 127, pp. 1723-1727 (1999).
T. Lachand-Robert and Mark A. Peletier, The Minimum of Quadratic Functionals of the Gradient on the Set of Convex Functions (72 kB), Calc. Var. Partial Differential Equations, Vol. 15, pp. 289-297 (2002).
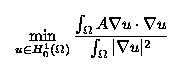
Some of these results are summarized in the Comptes Rendus paper T. Lachand-Robert and Mark A. Peletier,Minimisation de fonctionnelles dans un ensemble de fonctions convexes, C. R. Acad. Sci. Paris, t. 325, Série I, p. 851-855 (1997).