
| Mapping the earth is a classic problem. For thousands of years
cartographers, mathematicians, and inventors have come up with methods
to map the curved surface of the earth to a flat plane. The main
problem is that you cannot do this perfectly, such that both the shape
and size of the surface are depicted properly everywhere.
This has intrigued me for a long
time. Why not just take a map of a small part of the earth, which is
almost perfect, glue neighboring maps to it, and repeat this until the
whole earth is shown? Of course you get interrupts, but does this
matter? What does such a map look like?
To check this out, we developed myriahedral projections.
For a quick impression of myriahedral projections, see the video. Two minutes, no audio. |
 |
|
|
For a detailed answer what these maps look like and how to generate them, see:
Jarke J. van Wijk. Unfolding the Earth: Myriahedral Projections. The Cartographic Journal, Vol. 45, No. 1, pp.32-42, February 2008.
The article was awarded with the Henry Johns Award 2009, run by the British Cartographic Society with the support of Lovell Johns, for the best Cartographic Journal article in 2008. The Cartographic Journal is published by Maney Publishing (www.maney.co.uk). A story on myriahedral projections in New Scientist can be found here. |
The method
The method used is the same for each type of myriahedral projection:
A myriahedron is a polyhedron with a very large number of faces. For this reason, we call the results myriahedral projections. In step 2 and 3, this myriahedron is cut open and unfolded. The resulting maps have a large number of interrupts, but are (almost) conformal and conserve areas. Examples Now, dependent on which mesh is used and which strategy for labeling the edges, different maps are obtained. First, one can cut along parallels or meridians. We call these graticular projections, since they are based on the graticule. The resulting images resemble familiar map projections. |

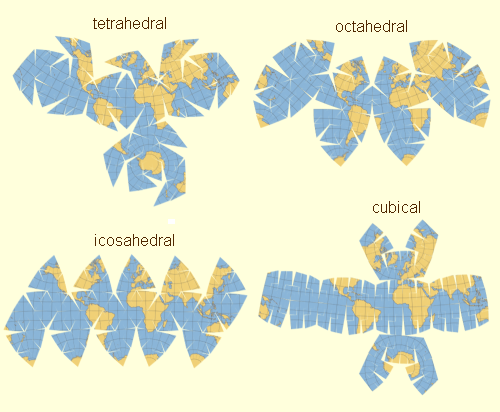
| Second, one can take a regular polyhedron, subdivide the faces, and fold it out. |
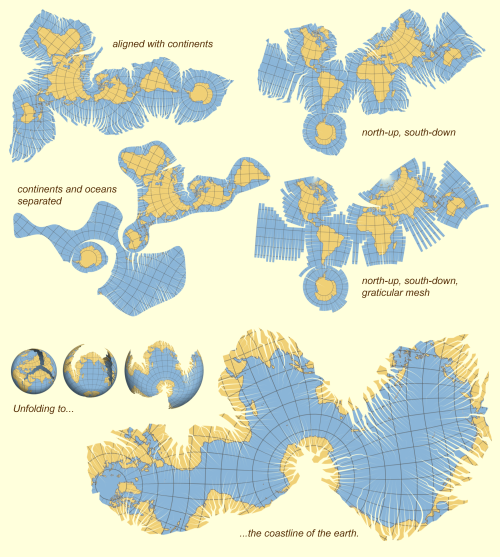
| One can take the shapes of the continents into account, when defining the cuts. By changing priorities, one can obtain maps where most cuts are through oceans or continents. |
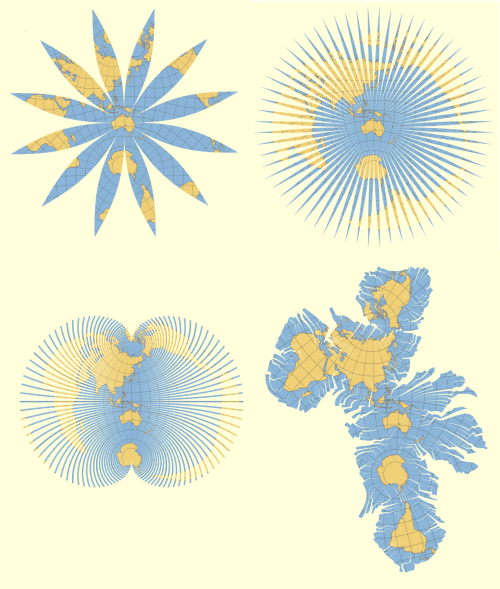
| Traditional maps are often Euro-centric. Focussing on for instance Australia gives different results (thanks to David Mayes for this suggestion). |
| For more information, see the paper or contact Jack van Wijk. All images copyright The British Cartographic Society 2008 and/or Jack van Wijk, TU/e. |
| I gratefully acknowledge Michiel Wijers, who has coined the term "myriahedral". I thank my colleagues, friends, and family for encouragement and advice, especially Jason Dykes and Menno-Jan Kraak. The website of Carlos Furuti gives much information on map projection. Flattening the Earth of John P. Snyder gives a great overview of the history of map projection. |