
| 
| 
|
|---|---|---|
| Bamboozle as it arrived in two pieces on 18 January 2013 | Finishing touches | Waiting to be installed |

| 
| 
|
| Installed | Installed (from below) | Installed (at an angle) |
Title Bamboozle Artists/Designers Koos Verhoeff and Tom Verhoeff Year 2012 Location Eindhoven University of Technology
Department of Mathematics & Computer Science
MetaForum (Opening hours)
1st floor, elevator hall near the receptionMaterial 19 mm polished acrylic Parts 51 equilateral triangles (30 cm side length; 15 yellow, 12 red, 12 green, 12 blue) Dimensions approx. 160 x 160 x 160 cm3 Installed 19 January 2013 Realization Glance & Vision, Veldhoven, NL



Bamboozle as it arrived in two pieces on 18 January 2013 Finishing touches Waiting to be installed 


Installed Installed (from below) Installed (at an angle)
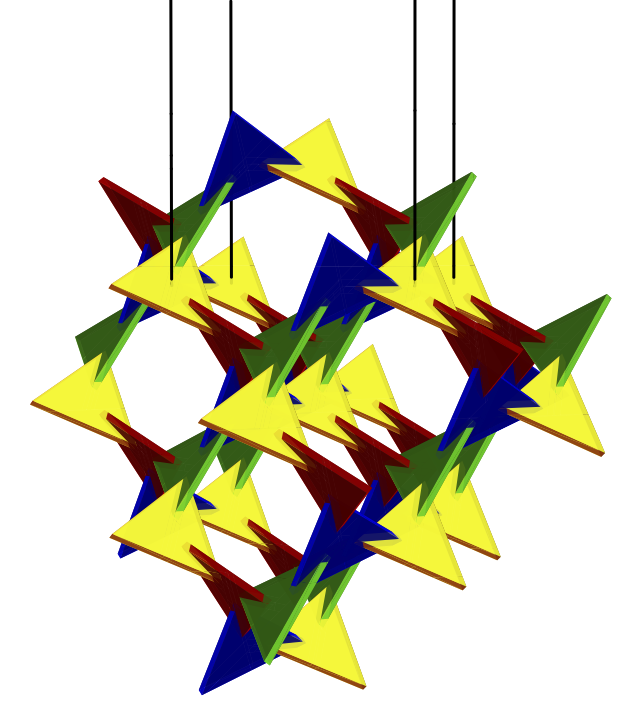
Bamboozle consists of 51 equilateral triangles, meeting pairwise at an angle of about 70.5 degrees (arccos 1/3). The four colors correspond to the four orientations of the triangles. There are 15 yellow triangles, and 12 triangles of each red, green, and blue. The smallest cycle involves 10 triangles.
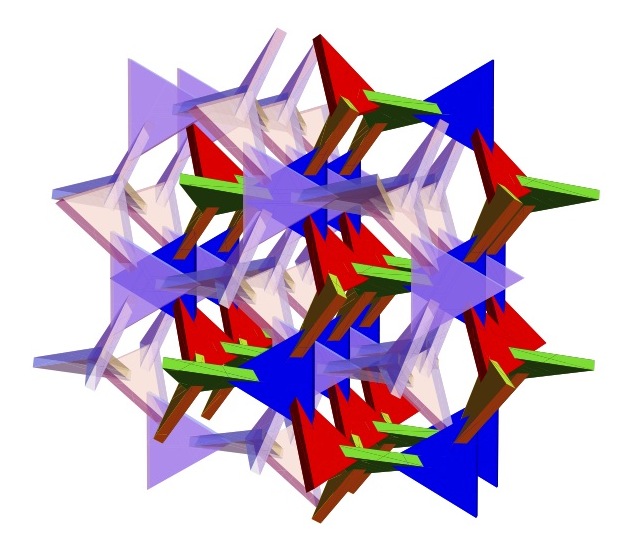
Bamboozle's structure is part of an infinite space-spanning structure with symmetry group I4332 (number 214 in the list of 230 3D space groups). This group contains rotations of order 2 (over 180 degrees) and order 3 (over 120 degrees), and also left-handed screw displacements of order 4 (over 90 degrees), and right-handed screw displacements of order 3. The group has no reflections; the structure is not mirror symmetric. However, the empty space surrounding the triangles has the mirror image as structure (symmetry group I4132); that is, a mirror image of the structure can be nicely woven through the structure itself (see picture below).
|
|---|
| Bamboozle with its mirror image interwoven |
The spatial structure is known by various names:
This structure is not well known, yet mathematically intriguing, and "ubiquitous" in nature [SH+al, TD]. For instance, it has the strong isotropy property [TS]. The only other structures with this property are diamond (in 3D) and the honeycomb lattice (in 2D; cf. graphene). As paraphrased by Tony Phillips,
[t]he strong isotropy property states that for any two vertices V and W of the crystal, any ordering of the edges adjacent to V and any ordering of the edges adjacent to W, there is a lattice-preserving congruence taking V to W and each V-edge to the similarly ordered W-edge.
Specially designed triangles slide into each other at the appropriate angle (see figure below).

| 
| 
| 
|
|---|---|---|---|
| Slotted triangles and how they slide together at an angle | |||
With a bit of consideration, you can construct a Bamboozle from 51 slotted triangles. Of course, you can also put together other shapes.
Technical details of these triangles:
| Side length | 30 mm |
|---|---|
| Thickness | 1.9 mm |
| Material | Nylon (White Strong & Flexible) |
| Production | 3D printed at Shapeways |
See [GH].
In [TV] we describe how Bamboozle was discovered.
Here is a short talk about Bamboozle:
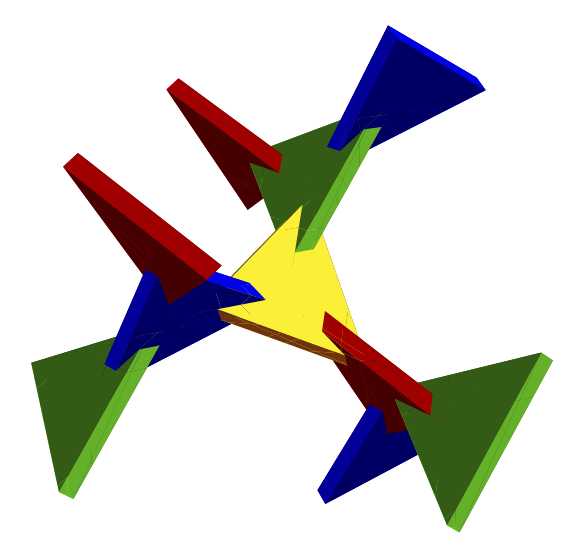
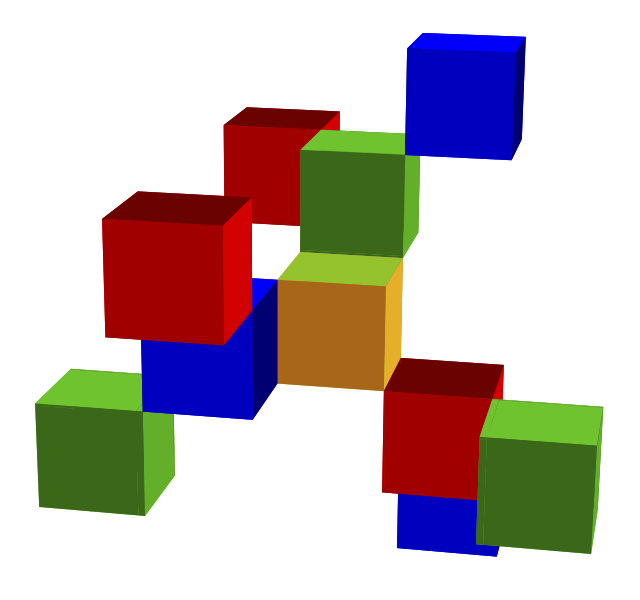
Bamboozle was generated by (see figures below)

| 
| 
| 
|
|---|---|---|---|
| Initial triangle | 1 generation added | 2 generations added | Cubes instead of triangles |
So, where does the name Bamboozle come from?
Koos Verhoeff gave this name, after we struggled some time to find out the mathematical structure.
bamboozle
verb
fool or cheat; confound or perplex
The Foundation MathArt Koos Verhoeff conserves and manages the artwork of Koos Verhoeff.