Up

Hamming graphs

Richard W. Hamming (1915-1998) did pioneering work in coding theory. The Hamming scheme is named after him. It is the association scheme where the elements are vectors of length d over some alphabet of size q. The relation (called Hamming distance) of two vectors is the number of coordinates where they differ.

The Hamming graph H(d,q) is the graph that describes the distance-1 relation in the Hamming scheme. It is the direct product of d complete graphs of size q. For d = 2 one gets the q×q grid, also known as the lattice graph of order q.

The Hamming graph H(d,q) is distance-regular of diameter d. In particular, for d = 2 it is strongly regular, and the parameters are v = q2, k = 2(q - 1), λ = q - 2, μ = 2.

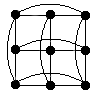
Example: H(2,3):

Lattice graphs

The graphs H(2,q) are also known as the Lattice graphs L2(q). They are uniquely determined by their parameters, except for q=4, in which case one has one more graph, the Shrikhande graph, with the same parameters.

The lattice graph L2(q) has independence number q and chromatic number q.

The complement of the lattice graph L2(q) also has independence number q and chromatic number q.

The lattice graph L2(3) is isomorphic to its complement. It is the Paley graph of order 9.

Spectrum

The Hamming graph H(d,q) has eigenvalues (q–1)d–qi with multiplicities (d choose i).(q–1)i for i=0,...,d.

The graph H(2,q) is uniquely determined by its spectrum when q is not 4.
The graph H(3,q) is uniquely determined by its spectrum when q is at least 36 (Bang-van Dam-Koolen), but not when q=3 or q=4. (There are four graphs with the spectrum of H(3,3), namely H(3,3), the graph on the lines of H(3,3), and two more. There are at least two graphs with the spectrum of H(3,4), namely H(3,4) and a Doob graph.)