Up

Paley graphs

Paley graphs are named after Raymond E.A.C. Paley (1907-1933). Paley was an MIT mathematician. He worked together with Norbert Wiener. He died in an avalanche in 1933 while skiing in the Canadian Rockies.

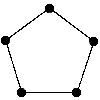
The graphs that bear his name are constructed as follows: Given a finite field F with q elements, make a graph with vertex set F where two vertices are joined when their difference is a square in the field. This is an undirected graph when q is congruent 1 (mod 4).

For q = 4t + 1, the parameters are v = 4t + 1, k = 2t, λ = t − 1, μ = t.

Examples (q = 5 and q = 9):

For q = 13 the Paley graph is locally a hexagon, so that the graph is a quotient of the hexagonal grid:

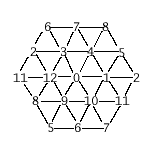
(More generally, the graph on the elements of GF(q), where q=6t+1, where x and y are adjacent when (y−x)6 = 1, is locally a hexagon, unless q is a power of 7.)

Paley graphs are isomorphic to their complements: if a is a nonsquare, then the map that sends x to ax is an isomorphism from the graph to its complement.

Independence and chromatic number

The independence numbers of the Paley graphs of prime order less than 7000 were computed by James Shearer. Geoffrey Exoo extended that table beyond order 16000.

In I. Broere, D. Döman, J. N. Ridley, The clique numbers and chromatic numbers of certain Paley graphs, Quaestiones Math. 11 (1988) 91-93, it is shown that when q is an even power of a prime, the clique and chromatic number are both sqrt(q). (Indeed, this is trivial: the subfield gives a clique, and its translates give a partitions into cliques. No larger cliques exist by the Hoffman bound. But the graph is self-complementary.)

A much stronger result is found in A. Blokhuis, On subsets of GF(q2) with square differences, Indag. Math. 46 (1984) 369-372. This paper shows that if a subset of GF(q) has size sqrt(q) and all differences are squares, or all differences are nonsquares, then the subset is the affine image of a subfield. In particular, this determines all cliques and all cocliques of size sqrt(q) in the Paley graph of order q.

Smaller maximal cliques are constructed in R. D. Baker, G. L. Ebert, J. Hemmeter, A. J. Woldar, Maximal cliques in the Paley graph of square order, J. Statist. Plann. Inference 56 (1996) 33-38, and in S. Goryainov, V. V. Kabanov, L. Shalaginov & A. Valyuzhenich, On eigenfunctions and maximal cliques of Paley graphs of square order, Finite Fields Appl. 52 (2018) 361–369.

For prime q, Hanson and Petridis improved the upper bound sqrt(q) to roughly sqrt(q/2), more precisely (1+sqrt(2q−1))/2. Equality holds for q=5, 13, 41.

A small table with independence numbers and chromatic numbers:

q 59131725 293741495361 73818997101109 113121125137149157 169173181193197
α 23335 445755 595656 7117777 138778
χ 33565 810971113 15918172119 171118202223 1322262825

The chromatic numbers for q=125,173,197 are due to Geoffrey Exoo (pers. comm.).

Dominating sets

The size of the smallest dominating set in the Paley graph P(q) is less than 1 + log q (found by picking greedily), and at least (0.5 − ε) log q (use the randomness of the Paley graph), where the logarithms have base 2. For q < 2048 one has:

sizeq
2 5
3 9-25
4 29-81
5 89-373, 401-409, 433, 457, 569, 953
6 389-397, 421, 449, 461-557, 577-941, 961-1213,
1229, 1249-1289, 1321, 1369, 1409, 1553, 1669
7 1217, 1237, 1297-1301, 1361, 1373-1381,
1429-1549, 1597-1657, 1681-2029

Similarly, for Paley tournaments P(q) one has:

sizeq
2 3
3 7-11
4 19-59, 103
5 67-83, 107-311, 343, 379
6 331, 347-367, 383-1151, 1171, 1223, 1331, 1723
7 1163, 1187, 1231-1327, 1367-1699, 1747-2039

Reference

Changwoo Lee, The domination number of a tournament, Kangweon-Kyungki Math. J. 9 (2001) 21-28.