The Petersen graph

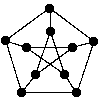
Julius Petersen (1839-1910) was a Danish mathematician. Around 1898 he constructed the graph bearing his name as the smallest counterexample against the claim that a connected bridgeless cubic graph has an edge colouring with three colours.

Construction

The Petersen graph is the complement of the Johnson graph J(5,2). Thus, it can be described as the graph with as vertex set the pairs from a 5-set, where two pairs are joined when they are disjoint. It is the unique strongly regular graph with parameters v = 10, k = 3, λ = 0, μ = 1, and has spectrum 3¹ 1⁵ (-2)⁴.

The Petersen graph is one of the Moore graphs (regular graphs of girth 5 with the largest possible number k² + 1 of vertices). Two other Moore graphs are known, namely the pentagon (k = 2) and the Hoffman-Singleton graph (k = 7). If there are other Moore graphs, they must have valency 57 and 3250 vertices, but cannot have a transitive group.

The Petersen graph is also a cage (graph with smallest possible number of vertices given its valency and girth).

Group

The full group of automorphisms is G = S₅ acting rank 3, with point stabilizer 2×S₃.

Supergraphs

The Petersen graph is contained in the complement of the Clebsch graph and the Sp(4,2) Generalized Quadrangle and the Hoffman-Singleton graph. Its extended bipartite double is contained in the Gewirtz graph.

Subgraphs

Substructures belonging to the maximal subgroups of the automorphism group:

a) A 4-coclique. There are 5 of these, forming a single orbit. The stabilizer of one is S₄, with vertex orbit sizes 4+6. The induced subgraph on the 6 is 3K₂.

b) A split into two pentagons. There are 6 of these, forming a single orbit. The stabilizer of one is 5:4, with vertex orbit size 10. There are 12 pentagons, with stabilizer D₁₀.

c) A vertex. There are 10 of these, forming a single orbit. The stabilizer of one is 2×S₃, with vertex orbit sizes 1+3+6.

Independence and chromatic number

The Petersen graph has independence number 4 and chromatic number 3. The five independent sets of size 4 are the sets of four pairs on a given symbol. The twenty 3-colorings are found by taking two independent sets of size four (they have one vertex x in common) and the remaining triple (the neighbours of x).

Circuits and Hamiltonicity

The Petersen graph is maximally non-Hamiltonian: there is a Hamiltonian path between any two nonadjacent vertices.

There are 12 pentagons, 10 hexagons, 0 heptagons, 15 octagons 20 nonagons and 0 decagons. The binary code spanned by the cycles is a [15,6,5]-code. The 64 code words are the zero word, the 12+10+15+20 = 57 cycles, and the 6 unions of two disjoint pentagons.

References

D. A. Holton & J. Sheehan, The Petersen graph, Australian Mathematical Society Lecture Notes 7, Cambridge University Press, 1993.

J. Petersen, Sur le théorème de Tait, L'Intermédiaire des Mathématiciens 5 (1898) 225-227.