Second Workshop on Infinitary Rewriting
Vienna, July 12, 2014
The morphism 0 -> 11, 1 -> 100000 from boolean streams to boolean streams has a unique fixed point; it may be obtained as the unique infinite
normal form of 1:S with respect to the following TRS:
S -> 0:0:0:0:0:f(S)
f(0:x) -> 1:1:f(x)
f(1:x) -> 0:0:0:0:0:f(x).
We give a turtle visualization as follows. The elements of the stream
are traversed consecutively: if the symbol 0 is read then the drawing direction is moved 90 degrees to the right; if the symbol 1 is read
then the drawing direction is moved 135 degrees to the left. In both cases after doing so a segment of unit length is drawn, and the drawing
continues in the end point of this segement. This yields a
picture consisting of infinitely many unit segments, starting as follows:
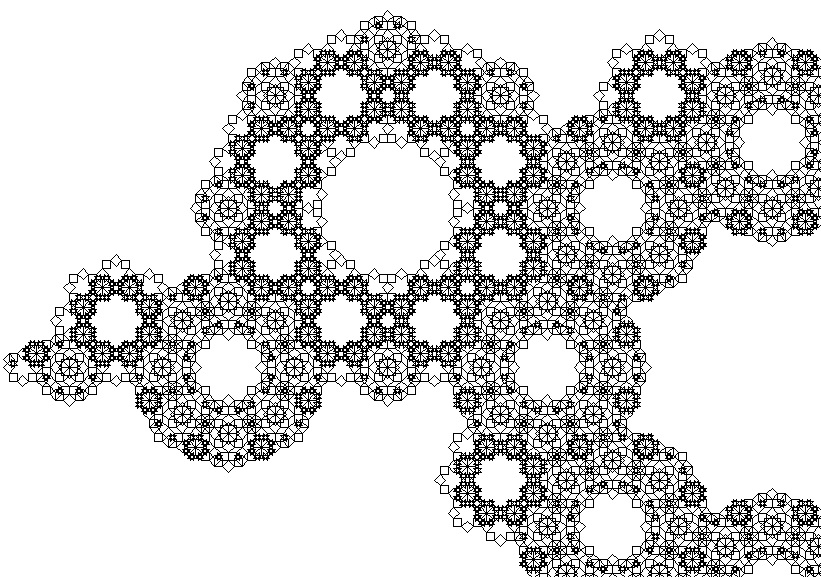
By instead taking the unique infinite normal
form of 1:S with respect to the following TRS:
S -> 0:0:0:0:0:0:f(S)
f(0:x) -> 1:1:f(x)
f(1:x) -> 0:0:0:0:0:0:f(x)
which is the unique fixed point of the morphism 0 -> 11, 1 -> 1000000 (so one more 0 for 1), and choosing 72 degrees to the left for 0 and
36 degrees to the left for 1, the following picture is obtained:

Contact information:
Hans Zantema, Eindhoven University of Technology, PO Box 513, 5600MB Eindhoven, The
Netherlands, email h.zantema@tue.nl.

