 |
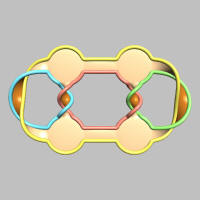
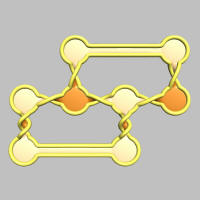
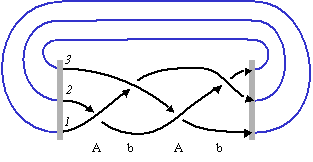
A braid consists of a number of parallel strands. These strands are braided step by step. At each step, two neighboring strands are twisted. A letter encodes how this is done. A letter A means that the first strand is twisted over the second, a letter B means that the second is twisted over the third, and so further. When lowercase is used instead of uppercase, the upper strand is twisted over the lower strand. Finally, when all strands are twisted, they are closed as shown in the figure above, without further crossings.
The braid diagram is shown in the user interface of SeifertView. Also, using the braid shape preset, a shape is generated that shows a circular braid diagram. Use an isometric view (tabsheet Display) to get the clearest picture.

Any knot or link can be represented via the braid notation, however, not always with a minimal number of crossings. An extension is provided to have some more flexibility. When a letter is followed by a number (say k), k twists in vertical direction are introduced in the braid. When no such number is given, k=1 is assumed. When this option is used, each letter (i.e., all a's, b's etc.) in the total code should be followed by either an even or an odd number. This extension is useful for instance to model so called Pretzel knots. As examples, below knots AA3A5, A2A2A2A2, and A2BA2B are shown.