
It is an old result that the number of nilpotent matrices with entries in GF(q) is qn(n−1). Proofs have been given by Philip Hall (1955), Fine & Herstein (1958), Gerstenhaber (1961), Crabb (2006) and others. In a more general setting (of which this is the GL(n,q), that is, An−1 case) Steinberg (1968) showed that the number of nilpotent matrices equals q|Φ|, where Φ is the root system. For example, the number of nilpotent skew-symmetric matrices is q2m(m−1) for n=2m, and q2m^2 for n=2m+1.
Clearly, for order 1 there is precisely 1. A little bit of work shows that the number of symmetric nilpotent matrices of order 3 equals q^3 + q^2 − q. Not so nice, but at least a polynomial in q. However, the number of symmetric nilpotent matrices of order 2 is 2q−1 for q=1 (mod 4), 1 for q=3 (mod 4), and q for q even. Not a polynomial in q. That means that we are doing something wrong.
If we choose a basis, then g is given by a matrix G, the Gram matrix of the basis, via g(x,y) = xT G y (with column vectors x,y). Let us call the form g for which G is the identity matrix the standard form. It is given by g(x,y) = Σ xiyi. A matrix is symmetric if and only if it is selfadjoint wth respect to the standard form.
For even q, the symplectic and standard forms are easily distinguished: for a symplectic form G has zero diagonal, for a standard form it has not.
For odd q, and even n, the standard form is the orthogonal direct sum of n/2 2-dimensional spaces with standard form. This 2-dimensional space is hyperbolic for q=1 (mod 4), elliptic for q=3 (mod 4). This means that V (with standard form) is elliptic when q=3 (mod 4) and n/2 is odd, and is hyperbolic otherwise.
Let us call these counts e(2m), h(2m), p(2m+1) (for odd q), and z(2m), s(2m), s(2m+1) (for even q).
Theorem. All of e(2m), h(2m), p(2m+1), z(2m), s(2m), s(2m+1) are polynomials in q.
Theorem. p(2m+1) = s(2m+1).
Put a(2m) = (h(2m)+e(2m))/2 and d(2m) = (h(2m)−e(2m))/2, so that h(2m) = a(2m)+d(2m) and e(2m) = a(2m)−d(2m).
Theorem. s(2m) = a(2m).
Theorem. z(2m) = q2m^2.
Theorem. p(2m+1) = q2ma(2m) + qmd(2m).
Theorem. p(2m+1) = (q2m−1)a(2m) + z(2m).
Theorem. a(2m) = q2m−1 p(2m−1).
This proves the corollary, conjectured by Sheekey:
Corollary. p(2m+1) = q2m−1 (q2m−1) p(2m−1) + q2m^2.
Conjecture.
(i) p(2m+1,2s+1) = [2m−2s] p(2m+1,2s).
(ii) a(2m,2s+1) = [2m−2s−1] a(2m,2s).
(iii) d(2m,2s) = [2m−2s] d(2m,2s−1).
(iv) [2m]a(2m,r) = [2m−r]p(2m+1,r).
(v) p(2m+1,2s) = qs(s+1) Π0≤i≤s−1 [2m−2i] . Σ0≤i≤s q(s−i)(2m−2s−1) Qnom(m−s−1+i,i,q2).
(vi) d(2m,2s+1) = (q−1)qm+s(s+1)−1 Π1≤i≤s [2m−2i] . Σ0≤i≤s q(s−i)(2m−2s−3) Qnom(m−s−1+i,i,q2).
Once more, as a picture:

so that
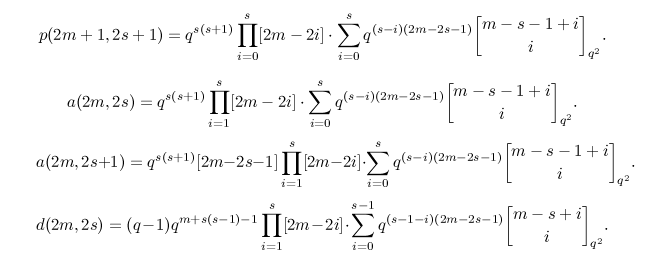
We can give an explicit recurrence for these functions. Let p0, h0, e0 count the selfadjoint nilpotent N such that Nx=0 for a fixed nonzero isotropic vector x. Define a0, d0 in the obvious way.
Proposition. These functions are recursively given by the following:
(i) [2m+1−r] p(2m+1,r) = [2m] p0(2m+1,r) + q2m(q−1) a(2m,r) + qm(q−1) d(2m,r).
(ii) [2m−r] a(2m,r) = [2m−1] a0(2m,r) + qm−1(q−1) d0(2m,r) + q2m−1(q−1) p(2m−1,r).
(iii) [2m−r] d(2m,r) = [2m−1] d0(2m,r) + qm−1(q−1) a0(2m,r) − qm−1(q−1) p(2m−1,r).
And for f any of p,h,e,a,d:
(iv) f0(n,r) = qr f(n−2,r) + (q−1)qr−1 f(n−2,r−1) + [n−r]qr−1 f(n−2,r−2).
Here f(n,r) = f0(n,r) = 0 for r < 0 or r > n or r = n > 0. As start of the induction only h(0,0) = 1 is needed.
Let An(X) = Σr a(n,r) Xr. Conjecture: A2m(−1/q) = q2m(m−2)+1.
Let Dn(X) = Σr d(n,r) Xr. Conjecture: D2m(−1/q) = −(q−1)qm(2m−3).
Suppose n > 0. Then the exponent is n iff the rank is n−1. The number of symmetric nilpotent matrices of order n and rank n−1 equals
p(2m+1,2m) = qm^2 [2] [4] ... [2m]for n = 2m+1. If q is odd and n=2m is even, then
a(2m,2m−1) = d(2m,2m−1) = qm(m−1) [m] [2] [4] ... [2m−2].So, twice this if the form is hyperbolic, 0 if the form is elliptic. For even q, the count is a(2m,2m−1) if the form is standard, and qm(m−1) [2] [4] ... [2m] if the form is symplectic.
Recursion via f0, as was done by Lusztig.
Recursion from all matrices to nilpotent matrices via Fitting decomposition, as done by Gow & Sheekey.
Send corrections, additions, theorems, proofs to aeb@cwi.nl.