where F is a single- or multiple-well potential. This equation, known also as the stationary Extended Fisher-Kolmogorov Equation or the stationary Swift-Hohenberg equation, has many solutions that are bounded on the real line.
The strut-on-foundation model leads to the ODE
![]()
where F is a single- or multiple-well potential. This equation, known
also as the stationary Extended Fisher-Kolmogorov Equation or
the stationary Swift-Hohenberg equation, has many solutions that
are bounded on the real line.
All activity described on this page is in collaboration with the Center for Nonlinear Mechanics in Bath, and most importantly Giles Hunt and Chris Budd.
The model of an elastic strut on an elastic foundation
produces the equation
above as the Euler-Lagrange equation associated with the
constrained minimization problem
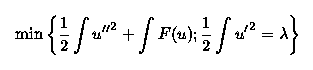
where we minimize the strain energy associated
with a deformation u under a constraint of prescribed
total shortening of the strut.
The parameter p, which arises as a Lagrange multiplier in this
minimization, is the load that is necessary to keep the deformed
strut in equilibrium.
In this paper we show that this minimization problem is
well-posed, i.e. that a minimizing sequence always converges to
a `nice' limit. Since we consider struts of infinite length, we can
also ask the question what happens when the shortening becomes large;
it turns out that for large lambda the minimizers of this problem
have a long periodic section, flanked by decaying tails.
As the next step in characterizing the selection of solutions by the minimization process we show in this paper that a minimizer necessarily has the aspect of a periodic function multiplied by an amplitude function that has a single maximum. Or more precisely, the sequence of local maxima of these oscillating solutions is first increasing, then decreasing. We call this generalized monotonicity. This result severely limits the set of potential solutions.
Rob Beardmore saw how the Lyapunov-Schmidt reduction could be used to construct branches of periodic solutions which have zero Hamiltonian. Together with some global analysis like in the Nonlinearity paper below and with numerical results by Chris Budd and Ahmer Wadee this gives a nice description of the bifurcation picture.
This paper arose as the result of the authors spending an afternoon together, finding out that from different points of view we had been working on very similar issues. The binding element is the combination of localized buckling (which can be viewed as a property related to small-amplitude behaviour) with subsequent large-amplitude restiffening. All three papers above fit in this class. Although slightly heterogeneous in nature, the paper gives a good feeling for the different aspects of these types of systems. Hint: don't try to print Fig. 6.
The combination of a monotonicity result for this type of Hamiltonian systems due to Toland, and an a priori estimate of bounded solutions due to L. A. Peletier & Troy, allows us in some cases to rule out, in a simple manner, solutions with a specific value of the Hamiltonian, based on the form of the potential F.