Home | Overview | Topics | Software | People | Bibliography | Other | Acknowledgments | How to cite
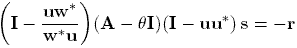
Origin
The Jacobi-Davidson method was proposed in 1996 by
Gerard Sleijpen and
Henk van der Vorst;
see [SVo96].
A reprint of this SIMAX paper appeared in 2000 in SIAM Review [SVo00].
The method combines ideas of the Davidson method [Dav75]
and Jacobi's method [Jac45], [Jac46],
stemming from 1975 and the 1840s (!), respectively.
Jacobi-Davidson as subspace method
Jacobi-Davidson is a subspace method for the eigenvalue problem, which
means that approximations to eigenpairs are sought from a subspace.
The main two stages in a subspace method are the
subspace extraction (how to get useful approximations from the subspace)
and the subspace expansion (how to expand the subspace).
Subspace extraction
The original paper [SVo96]
discusses the standard Rayleigh-Ritz and the harmonic Rayleigh-Ritz
[Mor91],
[PPV95],
[SVo96],
[Bea98],
[Ste01]
[SEs03]
as subspace extractions.
But the method can also be combined with refined Rayleigh-Ritz
[Jia97],
[FJi05],
or variations on the harmonic and refined Rayleigh-Ritz method
[Hoc05],
[Hocpp].
Subspace expansion
The subspace expansion of Jacobi-Davidson is done by approximately
solving a correction equation (cf. the "logo" at the top of this page).
See [Not02], [SEl02],
[Sta07a],
and [HNo09] for studies when to stop the inner iteration.
Instead of the usual vector projections, subspace projections have also been tried
for the correction equation [GSl99];
see also [SVM98].
Convergence properties have been studied in for instance
[Esh02],
[HSl03],
[Ovt03a],
[Ovt03b],
[FSp07].
Other important issues
Apart from the subspace extraction and subspace expansion,
in practice the Jacobi-Davidson may often need restarts
[SSa98],
and deflation
[FSV98b],
[Sta07b].
The possibility of preconditioning of the correction equation
is one of the key aspects and main advantages of Jacobi-Davidson: see
[Bas99],
[GSV00],
[GSV03],
[BPS03],
[SWu04],
[AGe05].
Parallelization is discussed in
[NPl99],
[NPl00],
[ABG06].
However the relatively common view that Jacobi-Davidson type methods can only
be competitive if a preconditioner is available may not be true in general---in
particular for generalized eigenvalue problems.
The parameters and options in Jacobi-Davidson (such as minimal and maximal dimension of the
search spaces, tolerance and/or number of iterations for the inner iteration,
the use of an initial Krylov space, thick restarts, etc)
may often have a reasonably large influence on its performance.
Special cases
Special attention has been devoted to the situation where the
eigenvalue problem is Hermitian or real symmetric
[SSa98],
[Bas99],
[Esh02],
[Geu02],
[Not02],
[BPS03];
real
[NRo07];
nonnormal
[Sta02],
[HSl03];
or complex symmetric
[AHo04],
[CAS05],
[Chi05].
Generalizations
Block variants of Jacobi-Davidson are discussed in
[Geu02],
[Bra03a].
The Jacobi-Davidson method has been generalized for various other eigenvalue
problems, including the generalized eigenvalue problem
[SBF96],
[FSV98b],
[HSl03],
[HNo07],
[Rom08];
the polynomial eigenvalue problem
[SVG96],
[SBF96],
[Mee00],
[TMe01],
[HSl03],
[HNo07],
[HSl08];
the multiparameter eigenvalue problem
[HPl02],
[HKP05];
the nonlinear eigenvalue problem
[BVo04],
[Vos04a],
[Vos04b],
[MVo04],
[Vos06],
[Vos07b];
the (generalized) singular value problem
[Hoc01],
[Hoc04],
[Hoc09];
and the product eigenvalue problem
[Hoc08].
Relations and comparisons with other methods
Apart from the connection with Jacobi's method and Davidson's method
(see also [Not05]),
the Jacobi-Davidson method also has relations with
the iterative improvement of approximate eigenvalues
[DMW83],
[Don83];
trace minimization
[SWi82],
[STo00];
differential-geometric approaches
[EAS98],
[LEl02],
[ASV04],
[BAG06],
[ABG06b],
[AMS08];
(inexact) Rayleigh quotient iteration
[SEl02],
[Not03];
(inexact) rational Krylov
[LMe99];
and the Riccati equation
[Bra03a],
[Bra03b].
Jacobi-Davidson can also be seen as an inexact Newton method
[SVo96b],
[FSV98a],
[HNo07].
Some more practically oriented comparisons with other methods are provided in
[AGe99],
[Mor00],
[AGe05],
[AHL05].
Use in applications
The Jacobi-Davidson has been used in various applications, including
pole-zero analysis
[Rom02],
[RBV04],
[RVM04],
[Rom07];
chemistry
[YPN01];
magneto-hydrodynamics (MHD)
[BFV96],
[NPl00];
electromagnetism, opto-electronics
[AGe99],
[NPl00],
[AGe01],
[Geu02],
[SWF02],
[AGe05];
oceanography
[DOW01],
[WDO03],
[DGh05],
[Dij05],
[Dij06];
and continuation
[Dor97].
In conclusion
In Jacobi-Davidson, the matrix is accessed only by
a matrix-vector product, which makes the method "matrix-free".
No exact (shift-and-)inverses are necessary; the correction equation needs
not be solved very accurately and may be preconditioned.
This makes the method attractive for interior eigenvalues of large sparse matrices,
in particular when a preconditioner is available.
More information
For more information on Jacobi-Davidson and other eigenvalue methods, see
the Bibliography and Topics pages and in particular the books
[BDD00],
[Ste01],
[Vor02]
and the review papers
[VGo97],
[Vor99],
[Sor02],
[Vor04],
[HNo06].
Competitive methods
See the Other links page for links to some competitive
methods such as
ARPACK and the
LOBPCG.