Both papers here tell the same story, but for different audiences.
The model that we use for the elastic strut embedded
in a viscous material is the following: the pair (u,P) satisfies
the differential equation
![]()
and the constraint condition, for every time t,
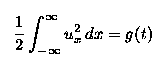
The first paper gives a derivation of this model. The first equation is a force
balance, the second specifies the `shortening' of the strut as a function
of time. This shortening is assumed to arise as the result of tectonic
compression and is generally believed to be the main reason why rock
folds in the first place. A typical function g(t) would therefore be slowly
increasing in time. The function P(t) can be seen as a Lagrange multiplier
associated with the constraint.
One thing we discovered in analysing the behaviour of an elastic strut embedded in a viscous material is that an initial deformation grows in amplitude if g(t) is constant or increasing. The folds develop more and more `wiggles' and the fold wavelength increases.
The equations admit a self-similar scaling, but those self-similar solutions that exist are not fit to be the long-term behaviour for solutions of the initial-value problem. As a result the solutions have an asymptotically self-similar long-term behaviour.
 Folds are a common feature of stratified rock. They have intrigued
geologists for ages, and to this day there are many aspects of
geological folding that are not well understood. The pictures shown
on this page show a small selection of the tremendous variety in forms
and structures. Besides being of intrinsic academic interest,
folds are also commonly associated
with valuable minerals, and the mining industry keeps a keen eye on
theoretical developments.
Folds are a common feature of stratified rock. They have intrigued
geologists for ages, and to this day there are many aspects of
geological folding that are not well understood. The pictures shown
on this page show a small selection of the tremendous variety in forms
and structures. Besides being of intrinsic academic interest,
folds are also commonly associated
with valuable minerals, and the mining industry keeps a keen eye on
theoretical developments.
