Computational Illumination Optics at TU/e
Designing the optical systems of the future

Designing the optical systems of the future

The Computational Illumination Optics group is one of the few mathematics groups worldwide working on optical design problems from illumination optics. The group has a healthy portfolio of PhD positions and close collaborations with industrial partners.
The group has three research tracks: freeform design, improved direct methods and imaging optics.
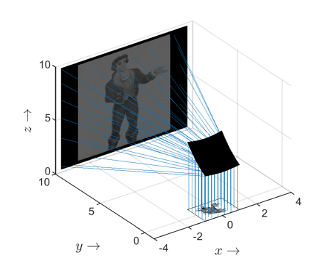
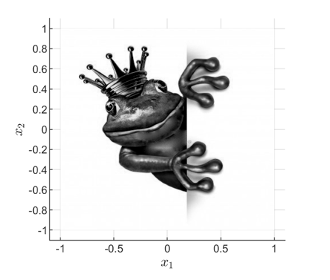
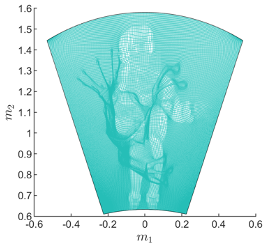
The goal in freeform design is to compute the shapes of optical surfaces (reflector/lens) that convert a given source distribution, typically LED, into a desired target distribution. The surfaces are referred to as freeform since they do not have any symmetries. The governing equation for these problems is a fully nonlinear PDE of Monge-Ampère type.
Key publication: Anthonissen, M. J. H., Romijn, L. B., ten Thije Boonkkamp, J. H. M., & IJzerman, W. L. (2021). Unified mathematical framework for a class of fundamental freeform optical systems. Optics Express, 29(20), 31650-31664. https://doi.org/10.1364/OE.438920.
We have developed a framework to describe optical systems using generated Jacobian equations. The equations are solved numerically by an iterative least squares method.
 |
 |
 |
 |
With a double freeform lens design we first compute a surface to map the source to an intermediate target intensity. The second surface is computed using the final target intensity.
 |
 |
In computational illumination optics, we want to find an optical surface that maps a given source to a desired target distribution. The function describing the surface satisfies a nonlinear partial differential equation called the Monge-Ampère equation.
For the design of freeform optical systems the Monge-Ampère equation comes in two variants, elliptic and hyperbolic. Furthermore, for each variant and each system multiple distinct optical surfaces can be calculated. For elliptic solutions the freeform surfaces are either convex or concave and for hyperbolic solutions the surfaces are saddle-like as shown in the figures.
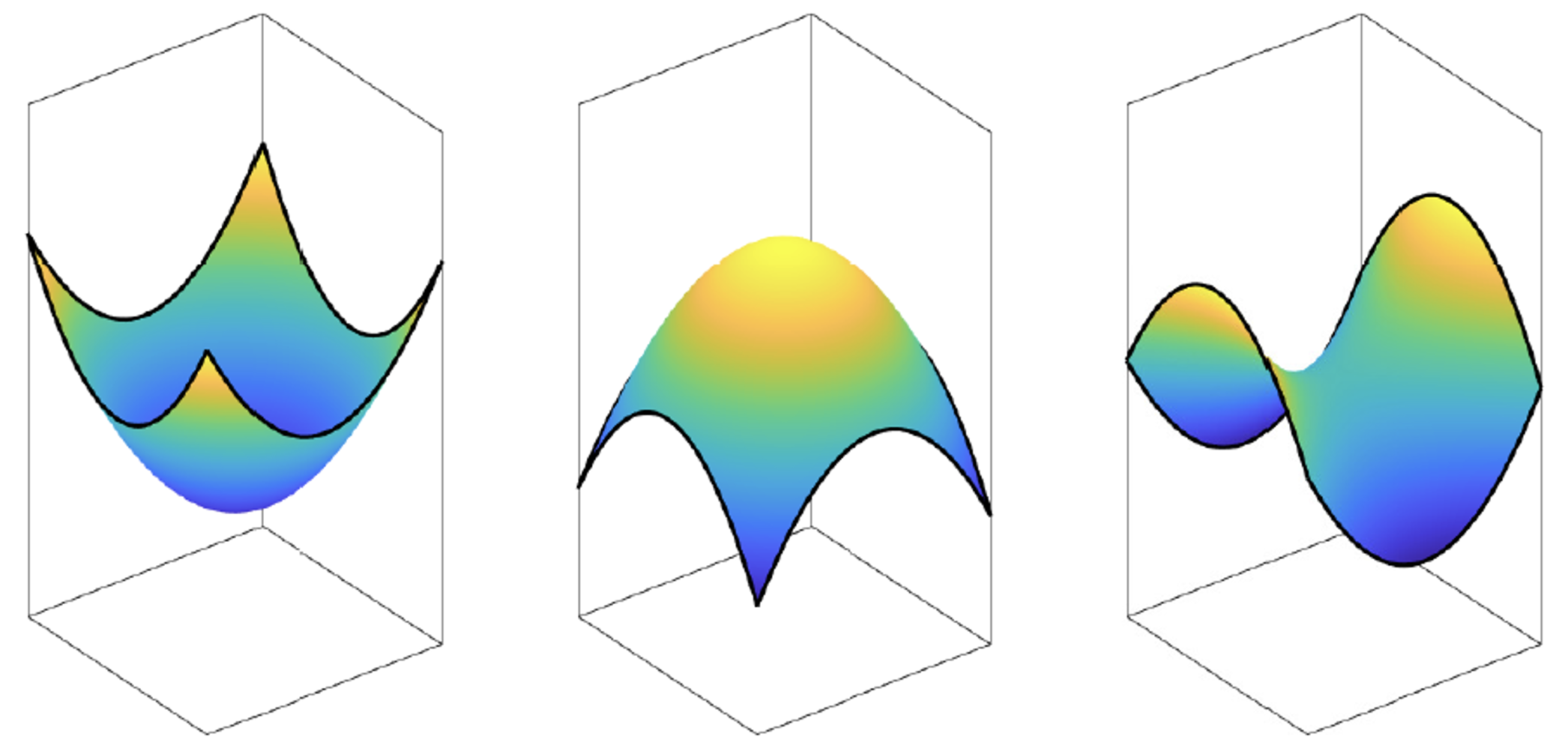
Consider now a lens array. Such an array consist of multiple LEDs, arranged in a grid-like structure, with lenses on top. In the figures the freeform optical surfaces of two such structure are shown. On the left only concave elements are used, while on the right convex, concave and saddle elements are used. The addition of saddle-like optical surfaces, and hence hyperbolic solution to the Monge-Ampère equation, allows for continuous optical surfaces while solely convex or concave surfaces, i.e., elliptical solutions, do not. This in term may lead to more compact optical systems.
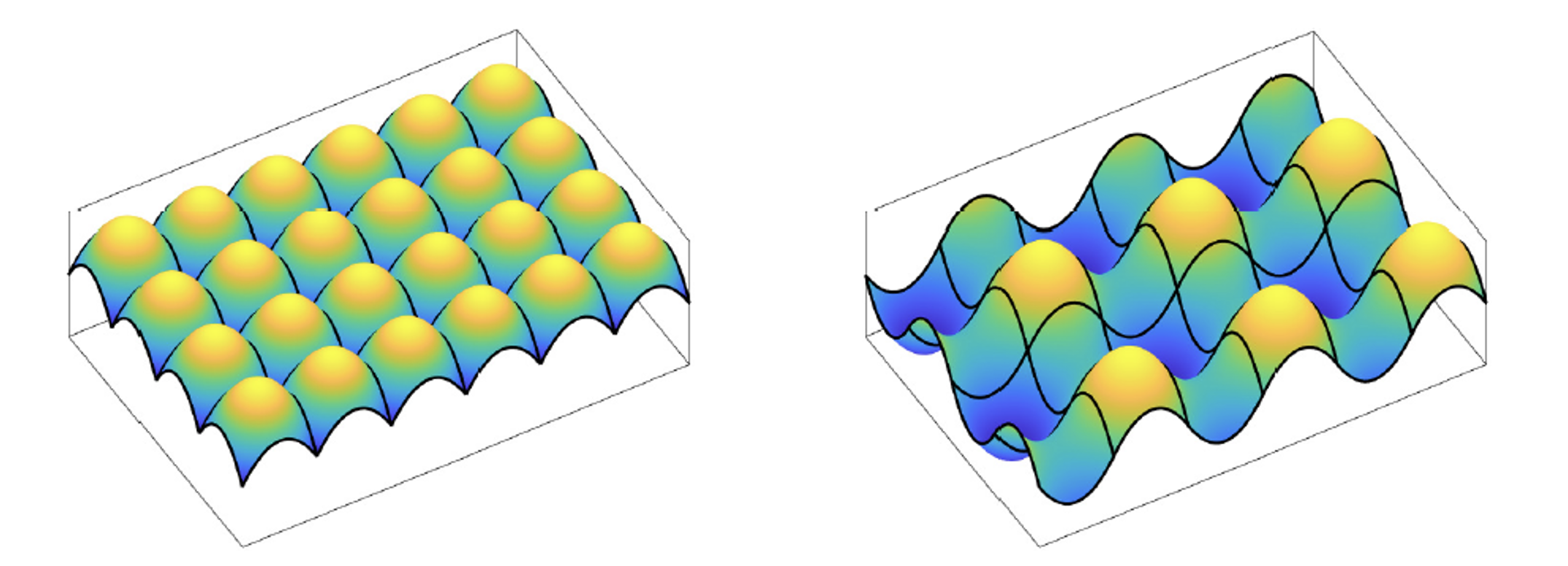
The increasing interest in the Monge-Ampère equation has significantly boosted the number of numerical methods for the elliptic Monge-Ampère equation, of which some have successfully been used to construct freeform optical systems. Unfortunately, the hyperbolic counter variant has received little attention. Therefore we work on developing methods for the hyperbolic Monge-Ampère equation and apply these to compute optical surfaces.
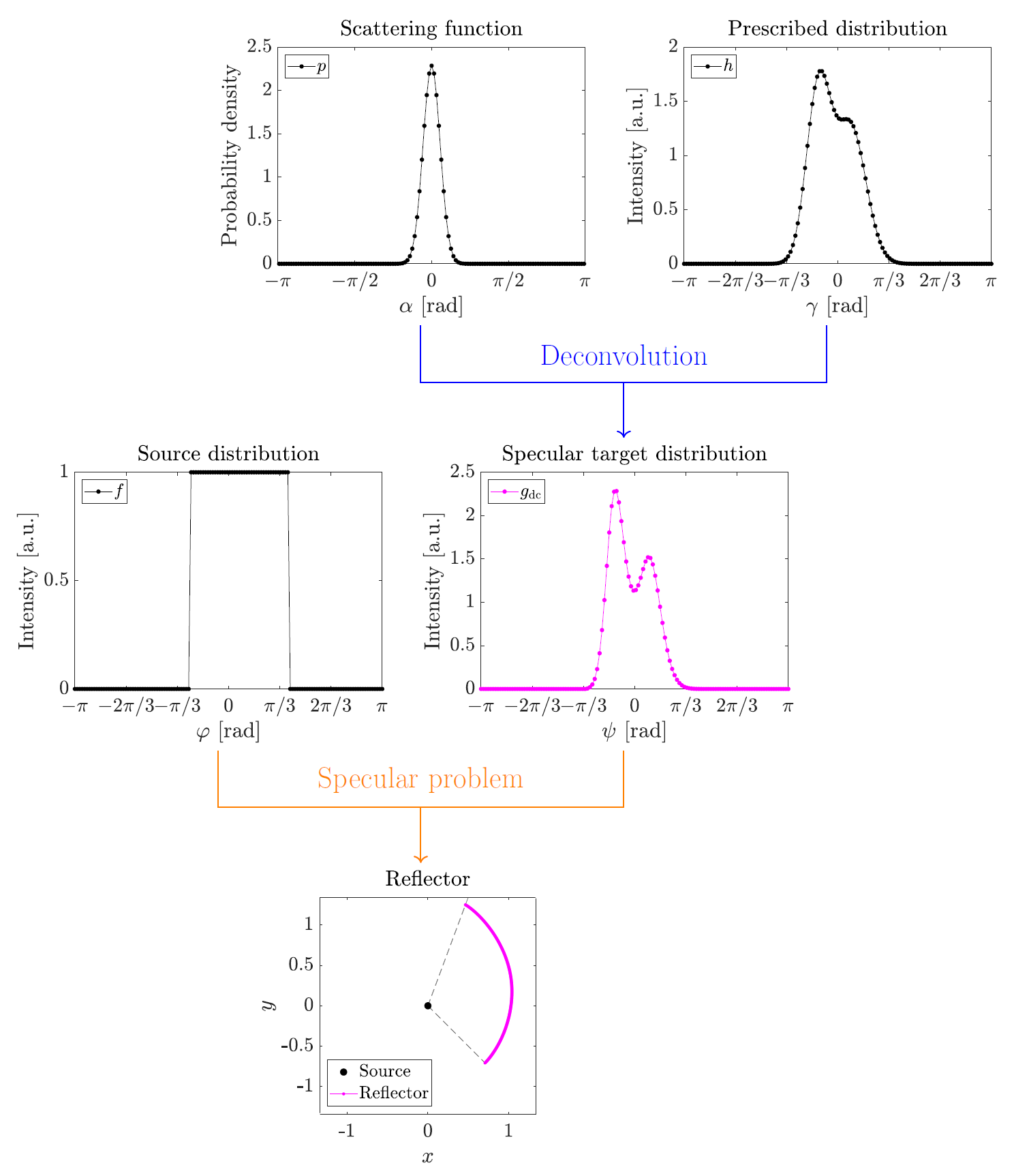
We aim to integrate surface scattering into freeform reflector design, i.e., the problem of computing a reflector which transforms a given source light intensity into a desired target light intensity. For this, a suitable model of surface scattering must be formulated. To do so, we first model the surface roughness using microfacets, i.e., small, tilted, specular (mirror-like) segments superimposed on the macroscopic reflector surface. We then consider the effect these have on the light scattered from the surface and find that, in two dimensions, the resulting expression is a so-called convolution integral equation between the function describing the orientations of the microfacets and a specular target distribution (in three dimensions it is instead a so-called Fredholm integral).
This mathematical approach to light scattering thus yields a direct way to compute the reflector surfaces by first solving the resulting integral equation for the specular target distribution and subsequently solving an inverse specular design problem. This is significantly easier than the original design problem since a specular surface (i.e., a perfect mirror) maps a single point from the source onto a single point in the target domain, as opposed to a scattering surface which maps one point on the source onto many points in the target domain.
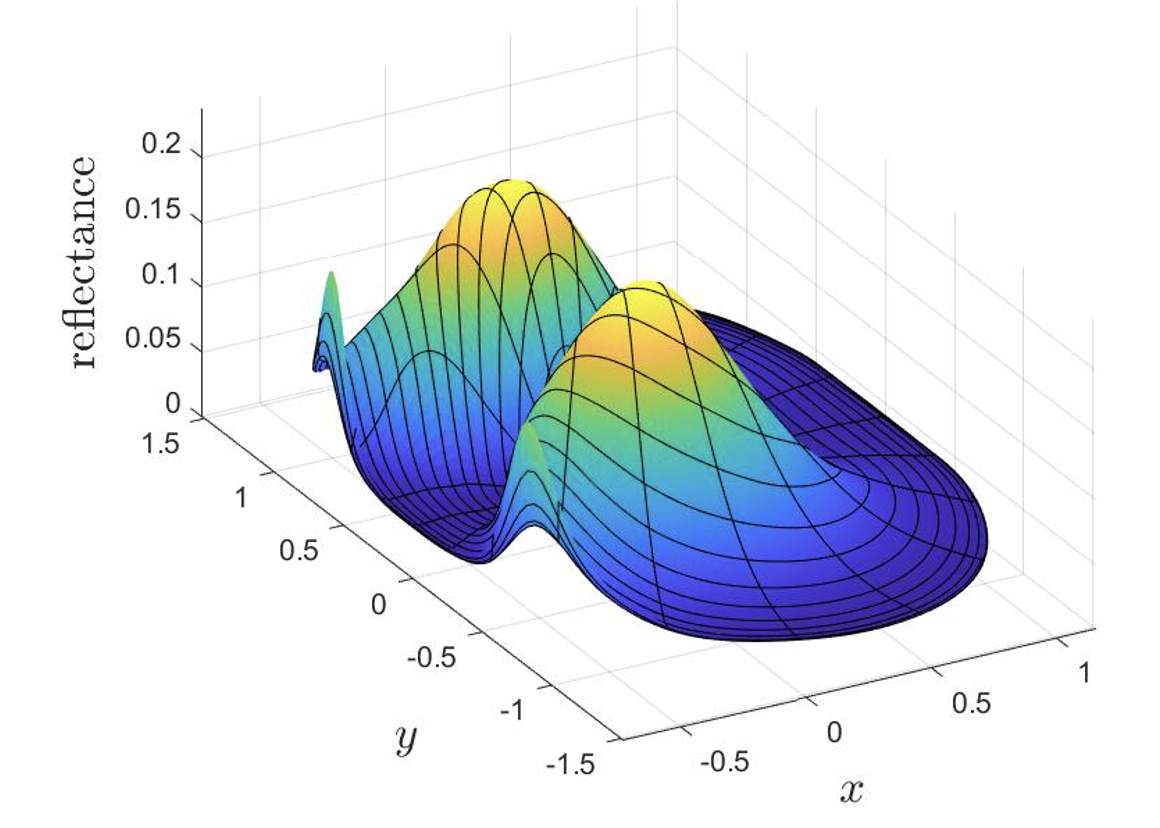
We have developed a method to design optical systems with two freeform reflectors for shaping a point source input into a collimated beam with a given distribution. This has application in, for example, lasers for manufacturing purposes. By freely choosing the output beam direction, we were able to make more compact reflector systems.
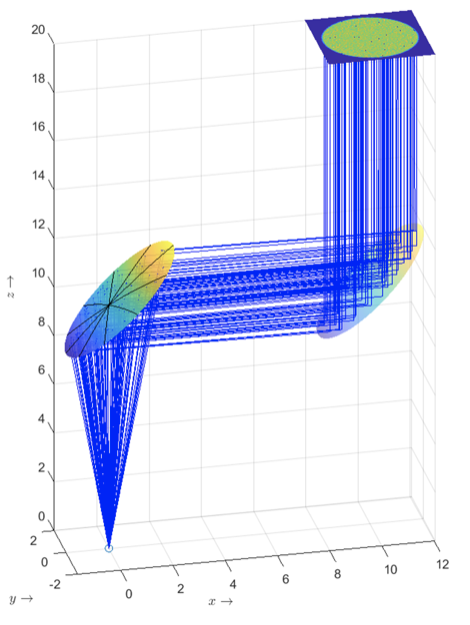
The output beam can be in any direction as is shown in the video below.
We are working on including Fresnel reflections in the design of lenses. At any optical interface, a part of the light is transmitted, while a part is reflected. The fraction depends on the material and the angle at which light hits the surface. In freeform design, this is generally ignored and only considered later in the design process.
Our goal is to take these reflections into account already in the inverse design algorithm and to minimize the amount of light that is lost due to these reflections. Consequently, more efficient lighting systems can be designed.
Direct methods, such as ray tracing, compute the target distribution given the source distribution and the layout of the optical system. These methods must be embedded in an iterative procedure to compute the final design and are based on Monte-Carlo simulation. They are known to have slow convergence.
Using the Hamiltonian structure of the system and advanced numerical schemes for PDEs, we are working on more efficient and accurate methods.
Key publication: van Gestel, R. A. M., Anthonissen, M. J. H., ten Thije Boonkkamp, J. H. M., & IJzerman, W. L. (2021). An energy conservative hp-method for Liouville’s equation of geometrical optics. Journal of Scientific Computing, 89, [27]. https://doi.org/10.1007/s10915-021-01612-x.
The standard way to simulate optical systems is ray tracing. Solving the Liouville equation is an alternative approach with huge advantages. It gives accurate results using far less computation time. Energy conservation is a key characteristic of the new numerical method.
Liouville's equation of geometrical optics governs the evolution of an energy density, the basic luminance, on phase space through an optical system. Combined with appropriate conditions at optical surfaces, describing reflection and refraction, the model is completed. The model is quite difficult to solve for, as the discretization of Liouville's equation involves discretizing a two-dimensional or four-dimensional phase space, besides the evolution coordinate, for two-dimensional and three-dimensional optics, respectively.
A novel solver for 2D optics was developed that uses discontinuous Galerkin (DG) methods. Multiple types of DG methods are used together and local time stepping is employed to provide a very efficient solver. With this new solver the basic luminance can be determined, and from this basic luminance both the illuminance and luminous intensity can be computed.
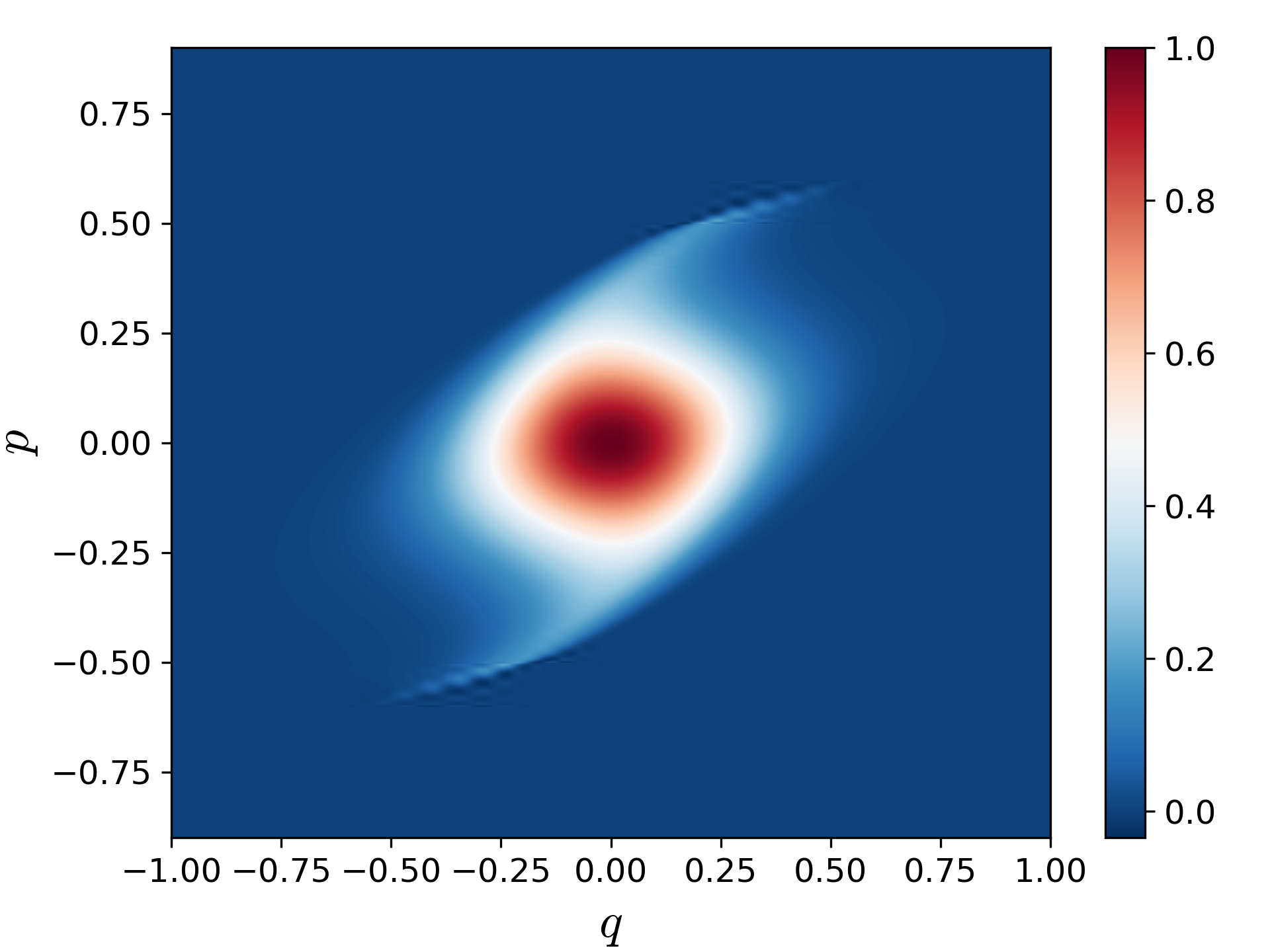
Ray tracing is used in non-imaging optics to calculate the light distribution at the target given an optical system and an initial distribution of rays at the light source. Every ray emitted from the source is followed until it reaches the target. The light source emits a large number of random rays into the optical system. A random ray distribution at the target is found by applying ray tracing to the initial set of random rays. From this distribution the target intensity can be calculated.
The phase space (PS) of an optical line in 2D is described by a set of position and direction coordinates. Every ray in PS is described by a point. The position coordinate is the x-coordinate of the intersection point between the ray and the optical line. The direction coordinate is the sine of the angle between the ray and the normal of the optical line. Each PS is divided into several regions corresponding to the different paths a light ray can follow. The target intensity can be calculated by only tracing rays that are on these borders. As a result less rays need to be traced compared to ray tracing.
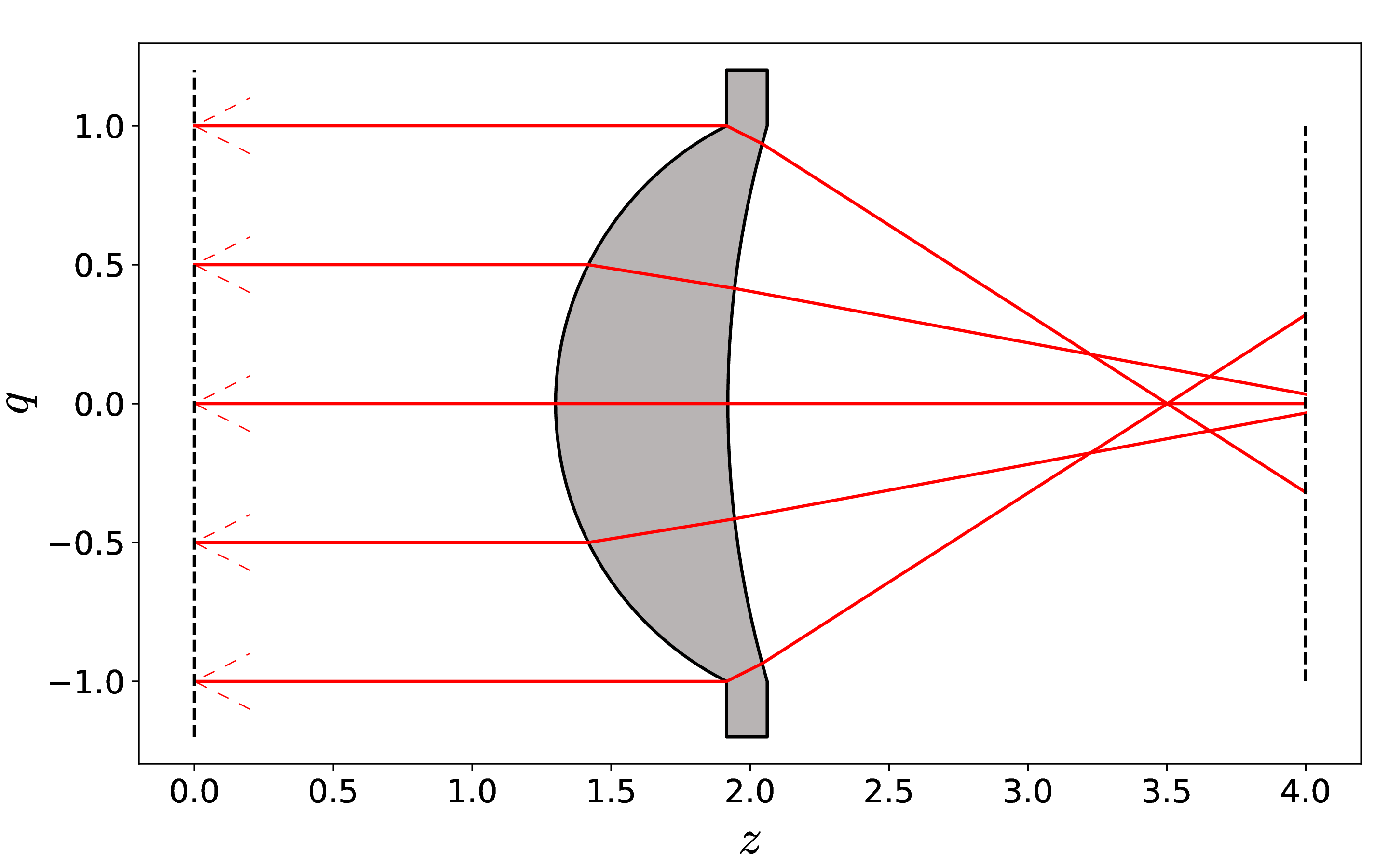
The third research track is imaging, where the goal is to form a very precise image of an object, minimizing aberrations. Light propagation is described in terms of Lie transformations.
Key publication: Barion, A., Anthonissen, M. J. H., ten Thije Boonkkamp, J. H. M., & IJzerman, W. L. (2022). Alternative computation of the Seidel aberration coefficients using the Lie algebraic method. Journal of the Optical Society of America A, Optics, Image Science and Vision, 39(9), 1603-1615. https://doi.org/10.1364/JOSAA.465900.
Optical systems are widespread in today’s society. They range from small devices, like phone cameras in everybody’s pockets, to large constructions, like telescopes in remote locations of our planet. These are examples of imaging systems, whose main goal is to produce an image of the desired object. Opposed to illumination optics, in imaging optics it is crucial to have ‘sharp’ images. Ideally, each light ray starting from one point on the object should converge to one single point on the image.
The truth of the matter is that having perfectly sharp images is not achievable. Small deviations are present for any optical system which result in the light rays converging not to one point but to an area on the image plane. The larger this spot on the image the less sharp the image will result. Deviations from the ideal image point are called aberrations.
We develop a mathematical model able to characterize and quantify said aberrations for an arbitrary optical system. Each optical element, e.g., a lens or a mirror, is associated with a mathematical element: a concatenation of Lie transformations. This mathematical construct contains all the information on how the optical element influences the path of the light rays.
With this mathematical description it is possible to shift our attention from the workbench of optical designers to pen and paper. In fact, adding a lens or mirror to the optical system on a workbench equates to concatenating additional Lie transformations to our expressions. This allows us to have explicit formulas for the path of the light rays and thus explicit formulas to describe the aberrations.
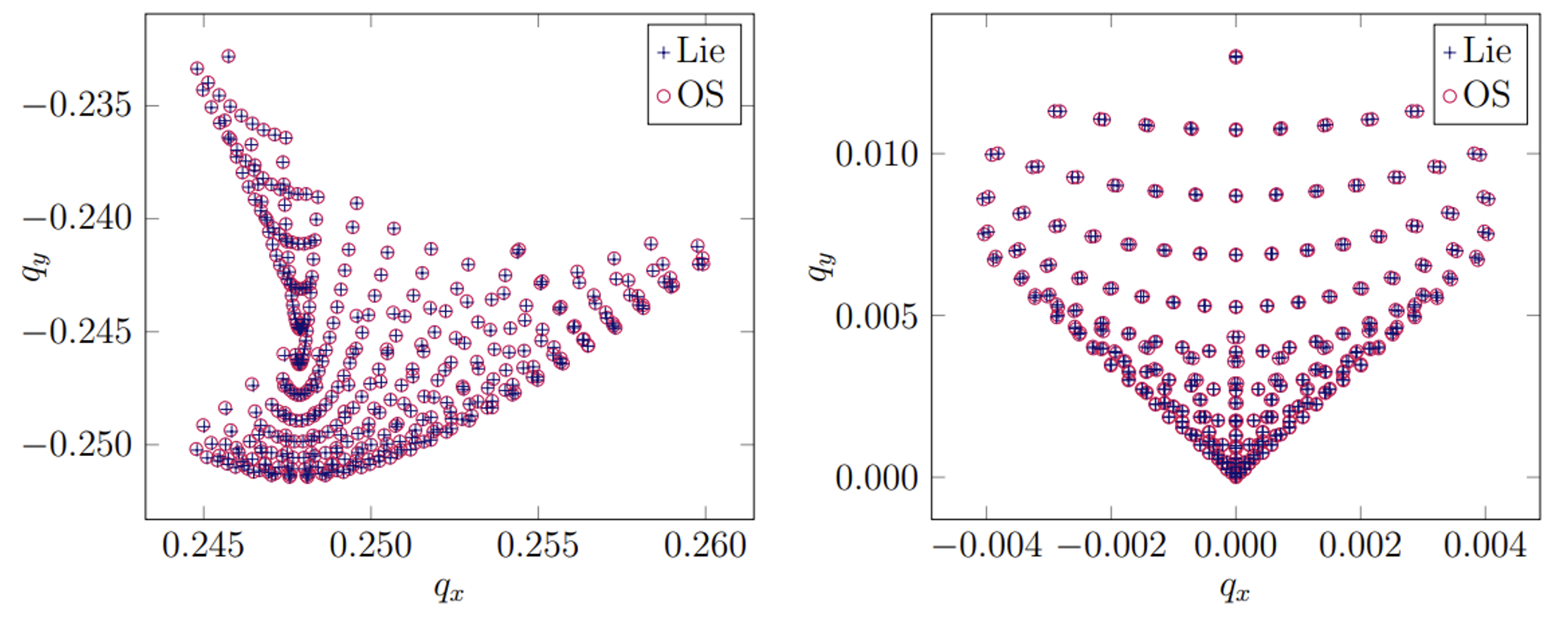
With the help of a systematic mathematical model for optical systems it is possible to gain additional insight to the complex phenomena of light refraction and reflection within optical systems. A thorough understanding of the underlying mathematical structure can enable us to apply additional mathematical concepts, for instance optimization algorithms, to design more compact and/or more precise optical systems than ever before.
So far we have used the proposed method to describe rotationally symmetric and plane-symmetric optical systems. Currently, we are investigating applications to GRIN lenses, like for instance optical fibers or the crystalline lens of the human eye.
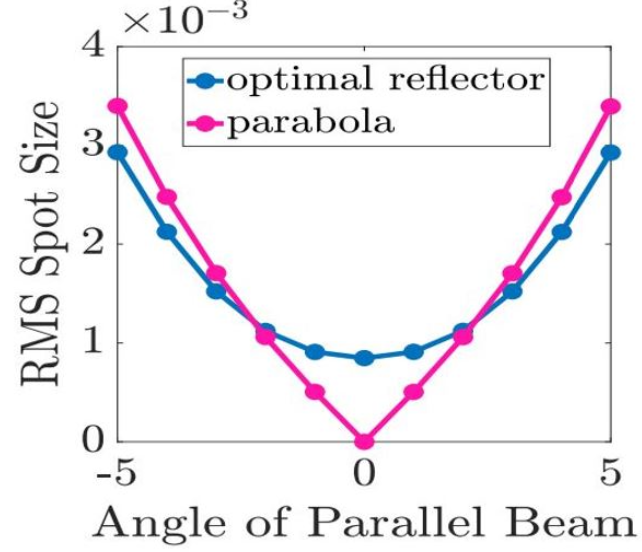
Recent technological advancements have stemmed an increasing demand for high quality imaging systems. Optical systems are inevitably prone to aberrations (small deviations from a perfect image), which affect the quality of an image adversely. Freeform surfaces are optical surfaces without any symmetry and are very suitable for correcting aberrations as they have multiple degrees of freedom.
In illumination optics, a freeform optical surface is computed for specified source and desired target light distributions. It is done by using a combination of an optical map and conservation of energy. This design methodology forms the basis of our research.
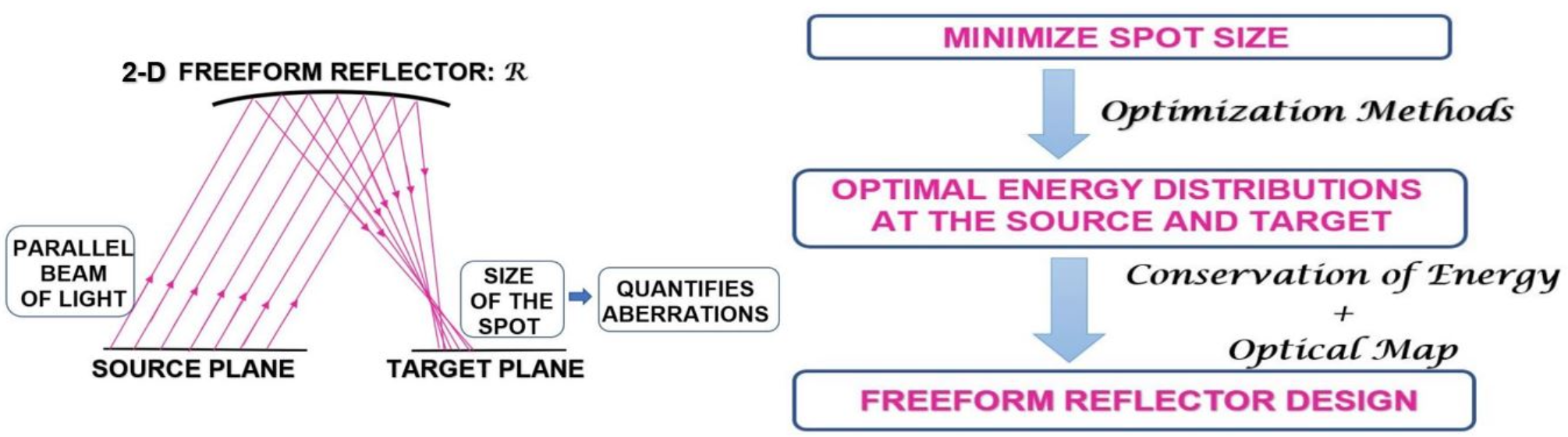
|
The aim of this research project is to develop optimization methods for freeform design to minimize aberrations in imaging systems. The idea is to find optimal energy distributions at source and target that enable us to design an optical system with one or more freeform reflector surfaces for aberration compensation. |