Computational Illumination Optics at TU/e
Designing the optical systems of the future

Designing the optical systems of the future

Nowadays LED devices are the standard in illumination optics, and optical systems are needed to create a desired light output of a luminaire. Optical systems typically consist of one or two optical surfaces, either reflectors or lens surfaces, that redirect light propagating through the system. The goal in illumination optics is to design optical systems that convert a given source LED distribution into a desired target distribution of, for example, car headlights. To achieve this, numerical design methods are required. This branch of optics is referred to as nonimaging illumination optics.
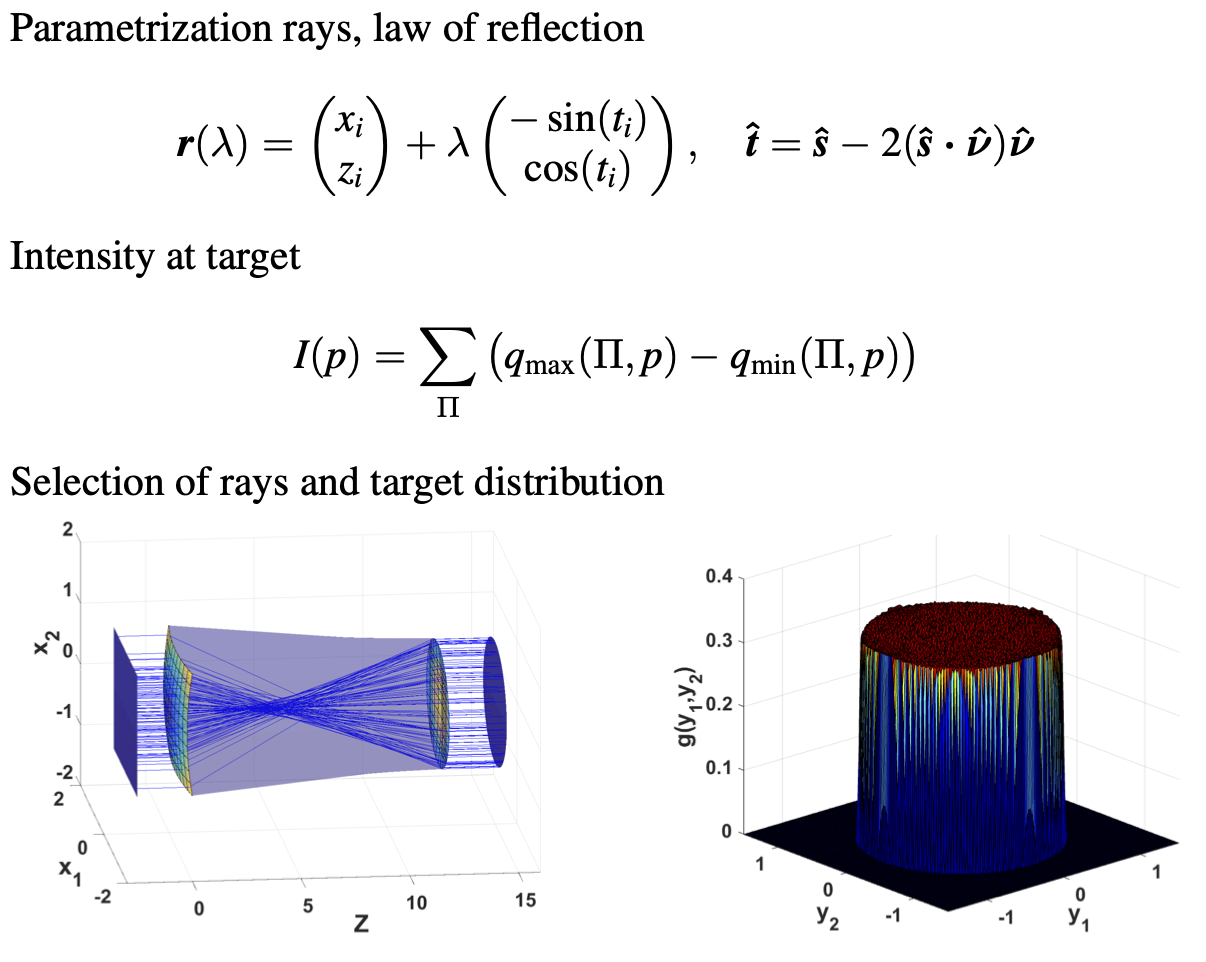
For the design of optical systems, there are basically two classes of methods, i.e., forward and inverse methods. In forward methods, we compute the target distribution given the source distribution and the layout of the optical system. Subsequently, we have to adjust the optical system in an iterative way to compute the desired target distribution. The prototypical method is ray tracing. In standard ray tracing we compute the paths of a large collection of rays from source to target, and from this we can compute the target distribution. Recently, we have developed an improved version of ray tracing, so-called backward ray mapping, which traces rays from target to source. An alternative to ray tracing is a Eulerian approach based on Liouville's equation, which is a linear advection equation in phase space where the notion of phase space is introduced. Rather than tracing a large number of rays through the system, we compute the propagation of energy carried by the rays through the system. For this equation many efficient numerical methods are available, and preliminary results show that this approach is superior to ray tracing.

On the other hand, in inverse methods, we directly compute the shape/location of a so-called freeform optical surface, given the source and target distributions. The underlying mathematical model is based on the principles of geometrical optics and energy conservation, giving rise to a fully nonlinear elliptic PDE, referred to as a generalized Monge-Ampère equation. We have derived PDEs for several optical systems and developed an efficient numerical solution method, which is state-of-the-art. Using inverse methods, we can compute optical surfaces that can create very complicated target patterns from a simple source distribution. As an example we have computed a lens surface that converts a parallel beam of light into the gray scale image of the painting Girl with a pearl earring.

All research projects are quite challenging, requiring new mathematical models and corresponding numerical methods. Moreover, this research is virgin territory in the applied mathematics community, therefore offering good opportunities for new research and publications. All projects are carried out together with Signify Research, and is therefore of direct importance for industry. Depending on your interest and/or expertise, the following topics could be investigated
This list is by no means exhaustive, and other research topics are possible as well.
As a spin-off, we intend to extend our research to imaging optics, in particular as used in photolithography. For this, we investigate optical systems that form a (high precision) image of the source. The purpose of our research is to design optical systems that minimize aberrations, i.e., distortions of the image. Also in this case numerical design methods are required. This research is highly explorative and we will investigate both forward and inverse methods. In forward methods, we determine the performance of an optical system by minimizing an object function defining the aberrations. On the other hand, in inverse methods, we can directly compute a freeform surface, given the source distribution and some condition on the optical system. We anticipate that we can adapt our Monge-Ampère models for this. These research projects are carried out in collaboration with ASML.