Symmetrieën tellen
De baan van een punt
-
Definitie `baan': alle hoekpunten waarin één hoekpunt kan overgaan
door een symmetrie toe te passen noemen we de baan van dat hoekpunt.
- Vierkant: de baan van $1$ bestaat uit $\{ 1, 2, 3, 4\}$. (Niet altijd bestaat de baan uit alle hoekpunten.)
- Vierkant: als we alleen de symmetrieën $(1)$ en $(13)(24)$ toelaten, bestaat de baan van $2$ uit $\{ 2, 4\}$.
-
Definitie `stabilisator van hoekpunt $h$': alle symmetrieën die
hoekpunt $h$ vastlaten, vormen de stabilisator van $h$.
- Vierkant: de stabilisator van hoekpunt $1$ bestaat uit $(1)$ en $(13)$.
- Vierkant: de stabilisator van $2$ bestaat uit $(1)$ en $(13)$.
Je kunt, net als bij het vierkant, bewijzen (waarbij $h$ een hoekpunt is): \[ |{\cal S}| = |{\cal S}_h| \cdot \hbox{|baan van $h$|} \] Hiermee kunnen we symmetrieën gaan tellen.
Hoe tel je?
- Kies een hoekpunt $i$
- Bepaal de grootte van de baan ${\cal B}$ van dit hoekpunt.
- Bepaal de stabilisator $G_i$ van dit hoekpunt. Dan geldt: is \[ |G| = |G_i| \cdot |{\cal B}| \]
Mocht je $G_i$ niet meteen kunnen bepalen, kies dan een hoekpunt $j$ dat niet vast blijft onder $G_i$ en herhaal het procédé.
Symmetrieën van een kubus
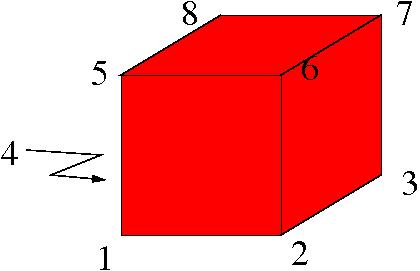
- De baan van een hoekpunt: je ziet eenvoudig dat de baan van een hoekpunt uit alle acht hoekpunten bestaat.
-
De stabilisator van een hoekpunt: als je hoekpunt $1$ vast laat,
dan moet hoekpunt $7$ ook vast blijven.
- De hoekpunten op afstand $1$ van hoekpunt $1$ blijven op afstand $1$. De symmetrieën die hoekpunt $1$ vastlaten, zijn symmetrieën van de resterende $6$ hoekpunten. De baan van hoekpunt $2$ bestaat uit $3$ hoekpunten: $2$, $5$ en $4$.
- De stabilisator van $1$ en $2$ laat ook $7$ en $8$ vast. De stabilisator bevat nog maar twee symmetrieën: de identiteit en de spiegeling $(4,5)(3,6)$.
- Zo vinden we \[ 8\cdot 3\cdot 2 = 48 \] symmetrieën van de kubus.
Symmetrieën van de kubus: een opsomming
Bij de kubus kun je de symmetrieën nog `meetkundig' begrijpen.
-
Rotaties: $24$
- Niets doen: $1$
- Rotaties om een as door de middelpunten van twee tegenover elkaar liggende zijvlakken: $3\times 3 = 9$ stuks. In permutatietaal bijvoorbeeld $(1234)(5678)$.
- Rotaties om een lichaamsdiagonaal: $4 \times 2 = 8$ stuks
- Rotaties om een as door middens van twee tegenover elkaar gelegen ribben: $6\times 1= 6$ stuks.
-
Spiegelingen: $24$
- Spiegelingen in vlakken op gelijke afstanden van twee tegenover elkaar liggende zijvlakken: $3\times 1 = 3$ stuks.
- Spiegelingen in vlakken door twee diagonalen: $4 \times 1 = 4$ stuks.
- Spiegelingen in vlakken door twee parallelle niet aangrenzende ribben: $6$ stuks
- Puntspiegeling in centrum: $1$
- Diverse draaispiegelingen...
Symmetrieën: alleen met hoekpunten?
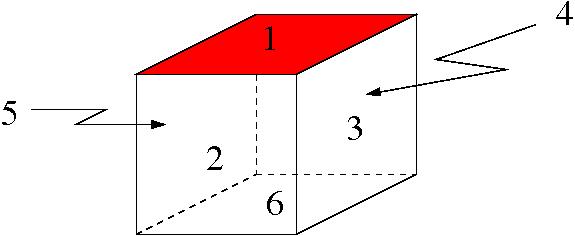
Soms is het handig andere aspecten van een object met getallen te labelen, bijvoorbeeld de zijvlakken van een kubus. Maar niet de nabuurschapsrelaties uit het oog verliezen!
- Er zijn $6$ zijvlakken: $1, \ldots , 6$.
- De baan van zijvlak `$1$': alle zes zijvlakken, dus $6$ elementen.
- Als zijvlak $1$ op dezelfde plaats blijft, heb je nog $8$ manieren om symmetrieën uit te voeren (net zoveel als voor het vierkant).
- Samen: \[ 6\times 8 = 48 (=2^3 \times 3!) \] symmetrieën.
- Ideeën over hogerdimensionale kubussen?