Spiegelingen in de ruimte en veelvlakken
Eindige spiegelingsgroepen
Tot nu toe heb je je beperkt tot het onderzoeken van de symmetrie van figuren in het vlak. Je kunt natuurlijk ook meetkundige figuren in de 3-dimensionale ruimte onderzoeken.
In deze sectie beperk je je weer tot figuren waarvan de symmetriegroep wordt voortgebracht door spiegelingen.
Een tweede beperking is dat je alleen nog maar naar figuren kijkt die een eindige symmetriegroep hebben!
Deze laatste beperking heeft tot gevolg dat er een punt in de ruimte is, dat wordt vastgelaten door alle symmetrieën van de symmetriegroep. Inderdaad, als $A$ een willekeurig punt van het vlak is $\sigma_1,\dots,\sigma_n$ zijn de $n$ verschillende symmetrieën in de symmetriegroep, dan geldt dat $$\sigma_1(A)+\sigma_2(A)+\dots+\sigma_n(A)$$ een punt in het vlak is dat wordt vastgehouden door elke $\sigma$ in de symmetriegroep. Immers, $\sigma\sigma_i$ is ook een symmetrie en dus gelijk aan $\sigma_j$ voor zekere $j\in \{1,\dots,n\}$, die uniek afhangt van $i$. En dat betekent dat $$\sigma(\sigma_1(A)+\sigma_2(A)+\dots+\sigma_n(A))=\sigma\sigma_1(A)+\sigma\sigma_2(A)+\dots+\sigma\sigma_n(A)=\sigma_1(A)+\sigma_2(A)+\dots+\sigma_n(A).$$
Als gevolg hiervan kun je dus aannemen dat het meetkundige figuur dat je onderzoekt gecentreerd is rond een vaste punt, zeg $O$. Alle spiegelvlakken horende bij spiegelingen in de symmetriegroep gaan dan door dit punt.
Nu neem een bol rond het punt $O$. Elk spiegelvlak van een spiegeling in de symmetriegroep snijdt de bol in een grote cirkel. De verschillende cirkels die zo ontstaan delen het boloppervlak op in eindig veel kleine stukjes. Zo'n stuk dat wordt begrensd, maar niet doorsneden, door deze cirkels, noem je, net als in de vorige sectie, een fundamentaalgebied. Je kunt de symmetriegroep nu weer onderzoeken door nader naar deze fundamentaalgebieden te kijken.
Als er maar één spiegeling in de symmetriegroep aanwezig is, dan wordt de bol in tweeën gedeeld.
Als elk van de fundamentaalgebieden door maar twee cirkels wordt begrensd, dan deel je de bol in gelijke partjes, net als een sinasappel of mandarijn.
Interessanter wordt het als het fundamentaalgebied wordt ingesloten door tenminste drie vlakken. Net als in de vorige sectie kun je inzien dat twee elkaar snijdende cirkels (of spiegelvlakken) een hoek met elkaar maken die gelijk is aan $\frac{\pi}{p}$ voor zekere gehele $p\geq 2$.
Maar, omdat we nu op een bol werken, is de som van de hoeken van een $k$-hoek met $k\geq 3$ niet meer gelijk aan $(k-2)\pi$ maar juist iets groter. Dus als het fundamentaalgebied een $k$-hoek is met hoeken ter grootte $\frac{\pi}{p_1}, \dots, \frac{\pi}{p_k}$, dan geldt $$\frac{1}{p_1}+\dots+\frac{1}{p_k}> k-2.$$ Maar dan geldt ook $$\frac{k}{2}\geq \frac{1}{p_1}+\dots+\frac{1}{p_k}> k-2$$ en dus. $$k>2k-4.$$ Je vindt dan ook dat $$k<4.$$ Een fundamentaalgebied is dus een driehoek op de bol.
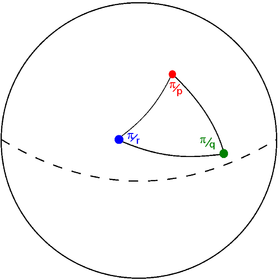
Verder kun je hier nog uithalen dat de drie hoeken van deze driehoek de waarden $\frac{\pi}{p},\frac{\pi}{q}$ en $ \frac{\pi}{r}$ aannemen, waarbij, als je aanneemt $p\geq q\geq r$, geldt dat $$\begin{array}{ll} (p,q,r)&= (p,2,2)\\ &= (3,3,2)\\ &= (4,3,2)\\ &= (5,3,2)\\ \end{array}.$$

|

|

|
Fundamentaalgebieden van type $(3,3,2)$, $(4,3,2)$ en $(5,3,2)$.
Het aantal elementen in de symmetriegroep
Neem een vast fundamentaalgebied $F$. Een symmetrie $\sigma$ beeldt het fundamentaalgebied $F$ af op een ander fundamentaalgebied, zeg $F'$, en is precies bepaald door dit beeld. Door herhaaldelijk spiegelingen toe te passen, is ook in te zien dat er voor elk fundamentaal gebied $F'$ een symmetrie $\sigma$ is die $F$ afbeeldt op $F'$. Dit houdt in dat het aantal symmetrieën in de symmetriegroep gelijk is aan het aantal fundamentaalgebieden. Je kunt dus het aantal symmetrieën in de symmetriegroep bepalen door het aantal fundamentaalgebieden te tellen. Dit aantal is natuurlijk gelijk aan de oppervlakte van de bol, gedeeld door de oppervlakte van $F$. Deze laatste oppervlakte kun je met behulp van integratie bepalen. Het gaat echter te ver dat hier uit te leggen. Deze berekening levert op:
| $(p,q,r)$ | Aantal symmetrieën |
| $(p,2,2)$ | $4p$ |
| $(3,3,2)$ | $24$ |
| $(4,3,2)$ | $48$ |
| $(5,3,2)$ | $120$ |
Regelmatige veelvlakken
Een regelmatig veelvlak is een 3-dimensionaal meetkundige figuur waarvan alle zijvlakken een regelmatige $k$-hoek vormen.
De kubus is een regelmatig veelvlak. Elk zijvlak is een vierkant. Naast de kubus bestaan nog 4 andere regelmatige veelvlakken, namelijk, de tetraëder, de octaëder, de isosaëder en de dodecaëder. Je ziet deze regelmatige veelvlakken in onderstaande plaatjes.
Net als in de vorige sectie kun je aantonen, dat de spiegeling in het vlak door het centrum van de figuur en de zijde van de zo'n regelmatige $k$-hoek een symmetrie van de hele figuur is. Dit betekent dat de regelmatige $k$-hoek, geprojecteerd op een bol, opgebouwd is uit een aantal fundamentaalgebieden.
Start je met een fundamentaalgebied van type $(p,2,2)$, dan kun je daar een regelmatige driehoek waarin alle hoeken (op de bol) de waarde $\frac{\pi}{2}$ hebben. Dit levert je een octaëder op.
Met een fundamentaalgebied van type $(3,3,2)$, kun je daar een regelmatige driehoek waarin alle hoeken (op de bol) de waarde $\frac{\pi}{3}$ hebben. Dit levert een tetraëder.
Met een fundamentaalgebied van type $(3,3,2)$, kun je zowel een regelmatige driehoek met rechte hoeken, als ook een regelmatige vierhoek met hoeken ter grootte $\frac{2\pi}{3}$. Je vindt de octaëder en de kubus.
Tot slot leveren fundamentaalgebieden van type $(5,3,2)$ driehoeken met hoeken ter grootte $\frac{2\pi}{5}$ of vijfhoeken met hoeken ter grootte $\frac{2\pi}{3}$ op. Je vindt de icosaëder en de dodecaëder.
Van links naar rechts: tetraëder, octaëder, kubus, icosaëder en dodecaëder.
Opdracht 1
Bepaal voor elk van de vijf regelmatige veelvlakken het aantal hoekpunten en het aantal zijvlakken.
Wat valt je op?