Vierkant: hoeveel symmetrieën?
Je kunt al de symmetrieën van een figuur proberen natuurlijk op te sommen. Maar, voor je daaraan begint wil je misschien wel weten hoeveel er zijn. Bekijk de symmetrieën van het vierkant.
- Ruwe schatting: hoekpunt $1$ zou op $4$ plaatsen terecht kunnen komen, voor hoekpunt $2$ zijn dan nog $3$ plaatsen vrij, voor hoekpunt $3$ dan nog $2$ plaatsen en voor hoekpunt $4$ is dan nog $1$ plaats vrij: \[ 4\cdot 3\cdot 2 \cdot 1 = 24 (=4!). \] Waarom is dit getal zeker te groot?
- Niet zo slim: alle permutaties éeéen voor éeéen bekijken en besluiten of het een symmetrie betreft. \[ (12): \hbox{ nee!}, \quad (13): \hbox{ ja!},\quad (1234): \hbox{ ja!},\ldots \] Lukt nog wel bij een vierkant ($24$ mogelijkheden nagaan), maar bij iets ingewikkelders...
Kan het slimmer?
Divide and Conquer!
- Divide: probleem opsplitsen in handige kleinere problemen
- Conquer: deelproblemen oplossen en daarmee het hele probleem
Wat is zo'n deelprobleem?
- Stap 1: als $1$ wordt vastgelaten, dan ook $3$
-
Stap 2: hoeveel symmetrieën zijn er die zowel $1$ als $3$
vastlaten?
$(1)$ niets doen: de triviale symmetrie, $(24)$: spiegeling
Dus er zijn twee symmetrieën die $1$ vastlaten.
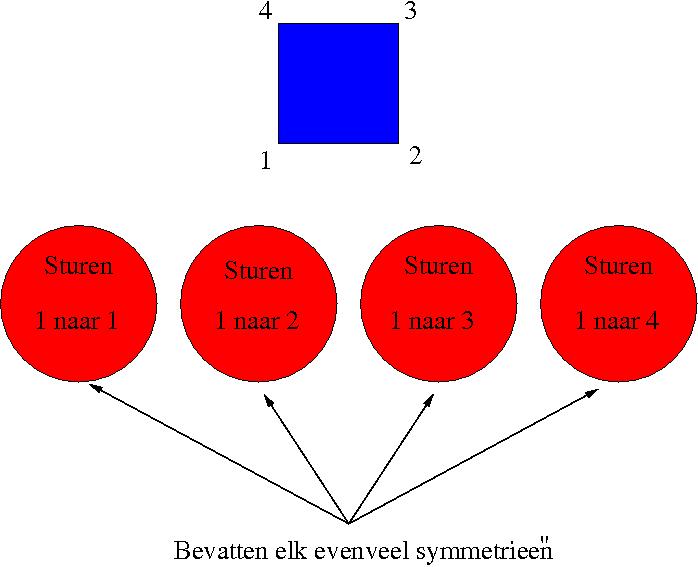
Splitsen in vier deelproblemen die erg met elkaar samenhangen.
- Hoeveel symmetrieën voeren $1$ in $1$ over, hoeveel $1$ in $2$, hoeveel $1$ in $3$ en hoeveel $1$ in $4$?
- Wat blijkt...? Allemaal even veel!
We tonen dit aan zonder ze eerst te tellen! En dezelfde techniek kunnen we in lastiger gevallen gebruiken.
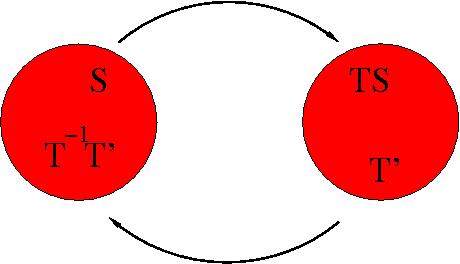
- Heen: als $S$ een symmetrie is die $1$ vastlaat en $T$ is een (even vaste) symmetrie die $1$ in $2$ overvoert, dan voert $TS$ hoekpunt $1$ in $2$ over: $TS(1)= T(S(1))=T(1)=2$, ofwel \[ 1\stackrel{S}{\longrightarrow} 1 \stackrel{T}{\longrightarrow} 2 \] Dus: bij elke symmetrie die hoekpunt $1$ vastlaat maken we er een die $1$ in $2$ overvoert.
- Terug: als symmetrie $T'$ hoekpunt $1$ in $2$ overvoert, dan laat $T^{-1}T'$ hoekpunt $1$ vast: \[ 1\stackrel{T'}{\longrightarrow} 2 \stackrel{T^{-1}}{\longrightarrow} 1 \] Dus: bij elke symmetrie $T'$ die $1$ in $2$ overvoert krijgen we er een die $1$ vastlaat.
- Conclusie: er zijn evenveel symmetrieën van de eerste als van de tweede soort. Net zo vinden we dat er van elke soort evenveel zijn. In elke soort zitten er dus $2$.
Samen: \[ 2\cdot 4 = 8 (=2^2 \times 2!) \] symmetrieën van het vierkant.