102. Kernelization Dichotomies for Hitting Subgraphs under Structural Parameterizations
July 11th 2024, Tallinn, Estonia
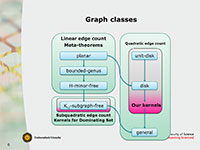
For a fixed graph H, the H-Subgraph Hitting problem consists in deleting the minimum number of vertices from an input graph to obtain a graph without any occurrence of H as a subgraph. This problem can be seen as a generalization of Vertex Cover, which corresponds to the case H = K_2. We initiate a study of H-Subgraph Hitting from the point of view of characterizing structural parameterizations that allow for polynomial kernels, within the recently active framework of taking as the parameter the number of vertex deletions to obtain a graph in a "simple" class C. Our main contribution is to identify graph parameters that, when H-Subgraph Hitting is parameterized by the vertex-deletion distance to a class C where any of these parameters is bounded, and assuming standard complexity assumptions and that H is biconnected, allow us to prove the following sharp dichotomy: the problem admits a polynomial kernel if and only if H is a clique. These new graph parameters are inspired by the notion of C-elimination distance introduced by Bulian and Dawar [Algorithmica 2016], and generalize it in two directions. Our results also apply to the version of the problem where one wants to hit H as an induced subgraph, and imply in particular, that the problems of hitting minors and hitting (induced) subgraphs have a substantially different behavior with respect to the existence of polynomial kernels under structural parameterizations.
101. Fixed-Parameter Tractable Certified Algorithms for Covering and Dominating in Planar Graphs and Beyond
June 12th 2024, Helsinki, Finland
A well-studied approach for dealing with NP-hard optimization problems is to resort to approximation algorithms, which output a solution that is provably close to an optimal one in polynomial time. This paper considers a different paradigm for coping with NP-hardness, which results in different guarantee on the given output: that it is an optimal solution for a small perturbation of the original instance. Formally speaking, for a positive real gamma >= 1, a gamma-certified algorithm for a vertex-weighted graph optimization problem is an algorithm that, given a weighted graph (G,w), outputs a re-weighting of the graph obtained by scaling each weight individually with a factor between 1 and gamma, along with a solution which is optimal for the perturbed weight function. We provide (1+epsilon)-certified algorithms for Dominating Set and Vertex Cover which, for any epsilon > 0, run in time f(1/epsilon) * n^(O(1)) on planar graphs. Our methods are conceptually simple: our algorithm is based on elementary local re-optimizations inspired by Baker's technique to obtain polynomial-time approximation schemes on planar graphs.
100. Fixed-Parameter Tractable Certified Algorithms for Covering and Dominating in Planar Graphs and Beyond
April 10th 2024, Asperen, The Netherlands
A well-studied approach for dealing with NP-hard optimization problems is to resort to approximation algorithms, which output a solution that is provably close to an optimal one in polynomial time. This paper considers a different paradigm for coping with NP-hardness, which results in different guarantee on the given output: that it is an optimal solution for a small perturbation of the original instance. Formally speaking, for a positive real gamma >= 1, a gamma-certified algorithm for a vertex-weighted graph optimization problem is an algorithm that, given a weighted graph (G,w), outputs a re-weighting of the graph obtained by scaling each weight individually with a factor between 1 and gamma, along with a solution which is optimal for the perturbed weight function. We provide (1+epsilon)-certified algorithms for Dominating Set and Vertex Cover which, for any epsilon > 0, run in time f(1/epsilon) * n^(O(1)) on planar graphs. Our methods are conceptually simple: our algorithm is based on elementary local re-optimizations inspired by Baker's technique to obtain polynomial-time approximation schemes on planar graphs.
99. A faster parameterized algorithm to find k-secluded trees
October 24th 2023, Asperen, The Netherlands
We revisit the k-Secluded Tree problem. Given a vertex-weighted undirected graph G, its objective is to find a maximum-weight induced subtree T whose open neighborhood has size at most k. We present a fixed-parameter tractable algorithm that solves the problem in time 2^O(k log k) * n^O(1), improving on a double-exponential running time from earlier work by Golovach, Heggernes, Lima, and Montealegre. Starting from a single vertex, our algorithm grows a k-secluded tree by branching on vertices in the open neighborhood of the current tree T. To bound the branching depth, we prove a structural result that can be used to identify a vertex that belongs to the neighborhood of any k-secluded supertree T' = T once the open neighborhood of T becomes sufficiently large. We extend the algorithm to enumerate compact descriptions of all maximum-weight k-secluded trees, which allows us to count them as well.
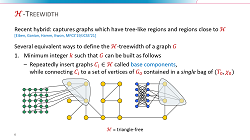
98. 5-Approximation for H-Treewidth Essentially as Fast as H-Deletion Parameterized by Solution Size
September 6th 2023, Amsterdam, The Netherlands
The notion of H-treewidth, where H is a hereditary graph class, was recently introduced as a generalization of the treewidth of an undirected graph. Roughly speaking, a graph of H-treewidth at most k can be decomposed into (arbitrarily large) H-subgraphs which interact only through vertex sets of size O(k) which can be organized in a tree-like fashion. H-treewidth can be used as a hybrid parameterization to develop fixed-parameter tractable algorithms for H-deletion problems, which ask to find a minimum vertex set whose removal from a given graph G turns it into a member of H. The bottleneck in the current parameterized algorithms lies in the computation of suitable tree H-decompositions.
We present FPT approximation algorithms to compute tree H-decompositions for hereditary and union-closed graph classes H. Given a graph of H-treewidth k, we can compute a 5-approximate tree H-decomposition in time f(O(k)) * n^{O(1)} whenever H-deletion parameterized by solution size can be solved in time f(k) * n^{O(1)} for some function f(k) >= 2^k.
The current-best algorithms either achieve an approximation factor of k^{O(1)} or construct optimal decompositions while suffering from non-uniformity with unknown parameter dependence. Using these decompositions, we obtain algorithms solving Odd Cycle Transversal in time 2^{O(k)} * n^{O(1)} parameterized by bipartite-treewidth and Vertex Planarization in time 2^O(k log k) * n^O(1) parameterized by planar-treewidth, showing that these can be as fast as the solution-size parameterizations and giving the first ETH-tight algorithms for parameterizations by hybrid width measures.
97. Kernels and Beyond
June 13th 2023, Bergen, Norway
Slides of an interactive session in which the status, relevance, and motivation for the most prominent open problems in kernelization are discussed based on experiences from people who have worked on them. The problems are: Directed Feedback Vertex Set, Vertex Planarization, Claw-free Edge Deletion, Interval Completion, Turing kernel for k-Path, Turing kernel lower bounds, Vertex Multiway Cut, and a linear-element kernel for d-Hitting Set.
96. New frontiers for graph drawing: Lossy (structural) kernelization and hybrid parameterizations
April 17th 2023, Dagstuhl, Germany
The talk covers three frontiers for the study of graph drawing problems from the perspective of parameterized complexity. The frontiers are illustrated by examples for 2-Layer Planarization, a fruitfly for parameterized graph drawing. Additionally, a sample result on each frontier is given based on my recent work.
The first frontier consists of kernelization for structural parameters. What is the strongest parameterization that admits a polynomial kernel? This question was recently resolved for the undirected Feedback Vertex Set problem, using the notion of elimination distance.
The second frontier is lossy kernelization, which aims to reduce instances in such a way that an approximate solution to the reduced instance can be lifted to a (slightly worse) approximation to the original. A constant-factor lossy kernel of polynomial size was recently developed for Vertex Planarization.
The last frontier consists of hybrid parameterizations improving simultaneously on parameterizations by solution size and treewidth. Fixed-parameter tractable algorithms for such parameterizations were recently found for Vertex Planarization. The running time of this algorithm is not much worse than for solution-size parameterizations.
95. Search Space Reduction Beyond Kernelization
December 12th 2022 (online talk)
The framework of kernelization gives a mathematical model for the rigorous analysis of preprocessing, aimed at showing that any instance with parameter k can efficiently be reduced to an equivalent one whose size depends only on k. Kernelization serves as a useful tool to obtain FPT algorithms, since any brute-force algorithm solves the reduced instance in time depending only on k. However, from the definition of kernelization it is not clear why kernelization would lead to significant speed-ups when the reduced instance is not solved by brute force, but by a fixed-parameter tractable algorithm whose running time is governed by the value of the parameter. To speed up such algorithms, it is the parameter controlling the size of the search space which should decrease, rather than the encoding size of the input. The discrepancy between reducing the instance size versus decreasing the search space is the focus of this talk. The quest for preprocessing algorithms that reduce the search space leads to a new type of algorithmic and graph-theoretical questions. The talk gives an introduction to this budding line of inquiry by presenting examples from recent work on the search for essential vertices and antler structures in graphs.
Based on joint work with Benjamin M. Bumpus, Huib Donkers, and Jari J.H. de Kroon.
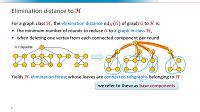
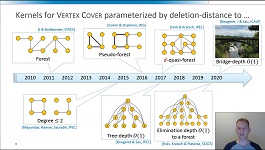
94. Vertex Deletion Parameterized by Elimination Distance and Even Less
November 30th 2022, Dagstuhl, Germany
The field of parameterized algorithmics was developed in the 90's to develop exact algorithms for NP-hard problems, whose running times scale exponentially in terms of some complexity parameter of the input but polynomially in the total size of the input. Many graph problems can be phrased as vertex-deletion problems: find a minimum vertex set whose removal ensures the remaining graph has a certain property. The Odd Cycle Transversal problem asks for the resulting graph to be bipartite; Feedback Vertex Set demands an acyclic graph. Through years of intensive research, these vertex-deletion problems are now know to be fixed-parameter tractable when parameterized by solution size: they can be solved efficiently on large inputs if the size of an optimal solution is small. Unfortunately, the requirement of having a small optimal solution is quite restrictive. We introduce a new paradigm for solving vertex-deletion problems based on recently introduced hybrid complexity-measures. This leads to algorithms to solve vertex-deletion optimally and provably efficiently on large inputs, as long as it is possible to obtain the target property in the input graph by a small number of rounds, where each round removes one vertex from each connected component. The resulting algorithms are obtained by combining new algorithms to decompose graphs into subgraphs which have the desired property and a small neighborhood, with dynamic-programming algorithms that employ such decompositions to find optimal solutions. The talk will discuss the motivation and main ideas in this approach, its connections to established concepts such as treedepth, generalizations to variants of treewidth, and give a high-level overview of our new decomposition algorithms.
Based on joint work with Jari J.H. de Kroon and Michal Wlodarzcyk at STOC 2021.
93. Exact algorithms for NP-hard problems: Search-space reduction for Odd Cycle Transversal
October 13th 2022, Eindhoven, The Netherlands
This 15-minute talk gives a brief insight in the type of questions I am currently pursuing, which relate to exact algorithms to solve NP-hard problems, based on the running example of the Odd Cycle Transversal problem. In the 70's, the research community believed that brute-force search was the best-possible algorithm to find an exact solution, which is only feasible when the input graph is small. In the 2000's, the advent of fixed-parameter tractability led to the viewpoint that the size of the solution (rather than of the graph) is what determines the complexity of an instance. The insight that was developed at ESA 2022 refines even this viewpoint: the vertices which are essential for making a 2-approximate solution can be identified by a search-space reduction phase, so that the combinatorial explosion required to find an optimal odd cycle transversal depends only on the number of vertices in an optimal solution which are, in some sense, fragile because they are not 2-essential.
Based on joint work with Benjamin M. Bumpus and Jari J.H. de Kroon.
92. Search Space Reduction Beyond Kernelization
September 20th 2022, Koper, Slovenia
The framework of kernelization gives a mathematical model for the rigorous analysis of preprocessing, aimed at showing that any instance with parameter k can efficiently be reduced to an equivalent one whose size depends only on k. Kernelization serves as a useful tool to obtain FPT algorithms, since any brute-force algorithm solves the reduced instance in time depending only on k. However, from the definition of kernelization it is not clear why kernelization would lead to significant speed-ups when the reduced instance is not solved by brute force, but by a fixed-parameter tractable algorithm whose running time is governed by the value of the parameter. To speed up such algorithms, it is the parameter controlling the size of the search space which should decrease, rather than the encoding size of the input. The discrepancy between reducing the instance size versus decreasing the search space is the focus of this talk. The quest for preprocessing algorithms that reduce the search space leads to a new type of algorithmic and graph-theoretical questions. The talk gives an introduction to this budding line of inquiry by combining examples from recent work with open problems for future research.
Based on joint work with Benjamin M. Bumpus, Huib Donkers, and Jari J.H. de Kroon.
91. Search Space Reduction Beyond Kernelization
May 5th 2022, Calpe, Spain
The framework of kernelization gives a mathematical model for the rigorous analysis of preprocessing, aimed at showing that any instance with parameter k can efficiently be reduced to an equivalent one whose size depends only on k. Kernelization serves as a useful tool to obtain FPT algorithms, since any brute-force algorithm solves the reduced instance in time depending only on k. However, from the definition of kernelization it is not clear why kernelization would lead to significant speed-ups when the reduced instance is not solved by brute force, but by a fixed-parameter tractable algorithm whose running time is governed by the value of the parameter. To speed up such algorithms, it is the parameter controlling the size of the search space which should decrease, rather than the encoding size of the input. The discrepancy between reducing the instance size versus decreasing the search space is the focus of this talk. The quest for preprocessing algorithms that reduce the search space leads to a new type of algorithmic and graph-theoretical questions. The talk gives an introduction to this budding line of inquiry by combining examples from recent work with open problems for future research.
Based on joint work with Benjamin M. Bumpus, Huib Donkers, and Jari J.H. de Kroon.
90. Vertex Deletion Parameterized by Elimination Distance and Even Less
December 6th 2021 (online talk)
The field of parameterized algorithmics was developed in the 90's to develop exact algorithms for NP-hard problems, whose running times scale exponentially in terms of some complexity parameter of the input but polynomially in the total size of the input. Many graph problems can be phrased as vertex-deletion problems: find a minimum vertex set whose removal ensures the remaining graph has a certain property. The Odd Cycle Transversal problem asks for the resulting graph to be bipartite; Feedback Vertex Set demands an acyclic graph. Through years of intensive research, these vertex-deletion problems are now know to be fixed-parameter tractable when parameterized by solution size: they can be solved efficiently on large inputs if the size of an optimal solution is small. Unfortunately, the requirement of having a small optimal solution is quite restrictive. We introduce a new paradigm for solving vertex-deletion problems based on recently introduced hybrid complexity-measures. This leads to algorithms to solve vertex-deletion optimally and provably efficiently on large inputs, as long as it is possible to obtain the target property in the input graph by a small number of rounds, where each round removes one vertex from each connected component. The resulting algorithms are obtained by combining new algorithms to decompose graphs into subgraphs which have the desired property and a small neighborhood, with dynamic-programming algorithms that employ such decompositions to find optimal solutions. The talk will discuss the motivation and main ideas in this approach, its connections to established concepts such as treedepth, generalizations to variants of treewidth, and give a high-level overview of our new decomposition algorithms.
Based on joint work with Jari J.H. de Kroon and Michal Wlodarzcyk at STOC 2021.
89. Vertex Deletion Parameterized by Elimination Distance and Even Less
April 22nd 2021 (online talk)
This talk contains a high-level overview of the some of the results in our recent work on vertex deletion. We describe a class of problem parameterizations for vertex-deletion problems which combine the best of two lines of fixed-parameter tractable algorithms: those based on the parameterization by solution size, and those based on parameterizations by graph-complexity measures such as treedepth and treewidth. The elimination distance of a graph G to a target class H is an example of such a hybrid parameterization. We describe our FPT-approximation algorithms for this parameterization, and how these can be used to find optimal solutions to the vertex-deletion problem to H.
Based on joint work with Jari J.H. de Kroon and Michal Wlodarczyk
88. Algebraic Sparsification for Decision and Maximization Constraint Satisfaction Problems
February 25th 2021 (online talk)
We survey polynomial-time sparsification for NP-complete Boolean Constraint Satisfaction Problems (CSPs). The goal in sparsification is to reduce the number of constraints in a problem instance without changing the answer, such that a bound on the number of resulting constraints can be given in terms of the number of variables n. We investigate how the worst-case sparsification size depends on the types of constraints allowed in the problem formulation (the constraint language), and how sparsification algorithms can be obtained by modeling constraints as low-degree polynomials. We also consider the corresponding problem for Maximum CSP problems, where the notion of characteristic polynomials turns out to characterize optimal compressibility.
Based on joint work with Hubie Chen, Astrid Pieterse, and Michal Wlodarczyk
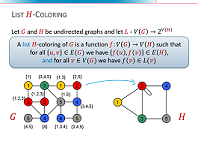
87. Sparsification Lower Bounds for List H-Coloring
December 17th 2020 (online talk)
We investigate the List H-Coloring problem, the generalization of graph coloring that asks whether an input graph G admits a homomorphism to the undirected graph H (possibly with loops), such that each vertex v in V(G) is mapped to a vertex on its list L(v). An important result by Feder, Hell, and Huang [JGT 2003] states that List H-Coloring is polynomial-time solvable if H is a so-called bi-arc graph, and NP-complete otherwise. We investigate the NP-complete cases of the problem from the perspective of polynomial-time sparsification: can an n-vertex instance be efficiently reduced to an equivalent instance of bitsize O(n^{2-epsilon}) for some epsilon > 0? We prove that if H is not a bi-arc graph, then List H-Coloring does not admit such a sparsification algorithm unless NP is in coNP/poly. Our proofs combine techniques from kernelization lower bounds with a study of the structure of graphs H which are not bi-arc graphs.
Based on joint work with Hubie Chen, Karolina Okrasa, Astrid Pieterse and Paweł Rzążewski
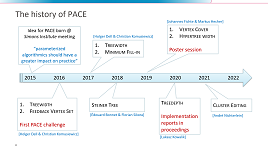
86. The 5th Parameterized Algorithms & Computational Experiments Challenge
December 17th 2020 (online talk)
A short presentation about the background of the PACE challenge, given at the start of the award ceremony of PACE 2020. The challenge dealt with the treedepth problem. For more information about the parameterized algorithms and computational experiments challenge, visit pacechallenge.org.
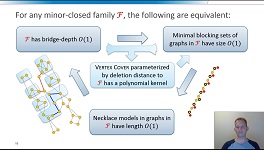
85. Bridge-Depth Characterizes which Structural Parameterizations of Vertex Cover Admit a Polynomial Kernel
July 20th 2020 (online talk)
We study the kernelization complexity of structural parameterizations of the Vertex Cover problem. Here, the goal is to find a polynomial-time preprocessing algorithm that can reduce any instance (G,k) of the Vertex Cover problem to an equivalent one, whose size is polynomial in the size of a pre-determined complexity parameter of G. A long line of previous research deals with parameterizations based on the number of vertex deletions needed to reduce G to a member of a simple graph class F, such as forests, graphs of bounded tree-depth, and graphs of maximum degree two. We set out to find the most general graph classes F for which Vertex Cover parameterized by the vertex-deletion distance of the input graph to F, admits a polynomial kernelization. We give a complete characterization of the minor-closed graph families F for which such a kernelization exists. We introduce a new graph parameter called bridge-depth, and prove that a polynomial kernelization exists if and only if F has bounded bridge-depth. The proof is based on an interesting connection between bridge-depth and the size of minimal blocking sets in graphs, which are vertex sets whose removal decreases the independence number.
Based on joint work with Marin Bougeret and Ignasi Sau
84. Bridge-Depth Characterizes which Structural Parameterizations of Vertex Cover Admit a Polynomial Kernel
July 8 – 11th 2020, Saarbrücken, Germany (online talk)
We study the kernelization complexity of structural parameterizations of the Vertex Cover problem. Here, the goal is to find a polynomial-time preprocessing algorithm that can reduce any instance (G,k) of the Vertex Cover problem to an equivalent one, whose size is polynomial in the size of a pre-determined complexity parameter of G. A long line of previous research deals with parameterizations based on the number of vertex deletions needed to reduce G to a member of a simple graph class F, such as forests, graphs of bounded tree-depth, and graphs of maximum degree two. We set out to find the most general graph classes F for which Vertex Cover parameterized by the vertex-deletion distance of the input graph to F, admits a polynomial kernelization. We give a complete characterization of the minor-closed graph families F for which such a kernelization exists. We introduce a new graph parameter called bridge-depth, and prove that a polynomial kernelization exists if and only if F has bounded bridge-depth. The proof is based on an interesting connection between bridge-depth and the size of minimal blocking sets in graphs, which are vertex sets whose removal decreases the independence number.
Based on joint work with Marin Bougeret and Ignasi Sau
83. Algebraic Sparsification for Decision and Maximization Constraint Satisfaction Problems
February 25th 2020, Krynica, Poland
We survey polynomial-time sparsification for NP-complete Boolean Constraint Satisfaction Problems (CSPs). The goal in sparsification is to reduce the number of constraints in a problem instance without changing the answer, such that a bound on the number of resulting constraints can be given in terms of the number of variables n. We investigate how the worst-case sparsification size depends on the types of constraints allowed in the problem formulation (the constraint language), and how sparsification algorithms can be obtained by modeling constraints as low-degree polynomials. We also consider the corresponding problem for Maximum CSP problems, where the notion of characteristic polynomials turns out to characterize optimal compressibility.
Based on joint work with Hubie Chen, Astrid Pieterse, and Michal Wlodarczyk
82. IPEC 2019 Business Meeting
September 12th 2019, Munich, Germany
81. Parameterized Complexity of Graph Coloring Problems
Graph Colouring: from Structure to Algorithms
July 3rd 2019, Dagstuhl, Germany
This talks surveys various aspects of the parameterized complexity of graph coloring problems. The goal is to understand how certain complexity parameters contribute to the difficulty of finding exact solutions to such problems. We discuss results in various parameterized algorithmic regimes, and point out open problems wherever possible. The regimes we consider are:
- Fixed-parameter tractable algorithms, for parameterizations that capture the structural complexity of the input graph. We will look at questions such as: if graph G is only k vertex deletions away from belonging to a graph class where coloring is easy, then can the coloring problem on G by solved in f(k)n^c time for some function f and constant c?
- Fixed-parameter tractable algorithms that work on a decomposition of the input graph. Given a graph G and a tree decomposition of width w, one can test the q-colorability of G in time O*(q^w), which is essentially optimal assuming the Strong Exponential Time Hypothesis. We will see how working over a linear layout of cutwidth w allows the problem to be solved much faster, by exploiting an interesting connection to the rank a matrix that encodes the compatibility of colorings on two sides of small edge cut.
- Fixed-parameter tractable algorithms for parameterizations that measure how far the input graph violates conditions that guarantee the existence of a good coloring. Brooks' theorem guarantees that any graph G that is not a clique or odd cycle, can be colored with \Delta(G) colors. Hence it is easy to test if a graph whose vertices have degree at most q, can be q-colored. How hard is it to test if G has a coloring with q colors, when only k vertices of G have degree more than q?
- Kernelization algorithms. Let k be a parameter that captures the structural complexity of the input graph - for example, the size of a minimum vertex cover. Is it possible to preprocess an input G in polynomial time, obtaining a graph G' of size polynomial in k, so that G has a 3-coloring if and only if G' has one? What is the best upper-bound on the size of G' in terms of k?
80. Sparsification for Constraint Satisfaction Problems
June 5th 2019, Bergen, Norway
We survey polynomial-time sparsification for NP-complete Boolean Constraint Satisfaction Problems (CSPs). The goal in sparsification is to reduce the number of constraints in a problem instance without changing the answer, such that a bound on the number of resulting constraints can be given in terms of the number of variables n. We investigate how the worst-case sparsification size depends on the types of constraints allowed in the problem formulation (the constraint language), and how sparsification algorithms can be obtained by modeling constraints as low-degree polynomials.
Based on joint work with Hubie Chen and Astrid Pieterse
79. Hamiltonicity below Dirac’s condition
May 6th 2019, Doorn, Netherlands
Dirac’s theorem (1952) is a classical result of graph theory, stating that an n-vertex graph (n >= 3) is Hamiltonian if every vertex has degree at least n/2. Both the value n/2 and the requirement for every vertex to have high degree are necessary for the theorem to hold. In this work we give efficient algorithms for determining Hamiltonicity when either of the two conditions are relaxed. More precisely, we show that the Hamiltonian cycle problem can be solved in time c^k n^{O(1)}, for a fixed constant c, if at least n-k vertices have degree at least n/2, or if all vertices have degree at least n/2-k. The running time is, in both cases, asymptotically optimal, under the exponential-time hypothesis (ETH). The results extend the range of tractability of the Hamiltonian cycle problem, showing that it is fixed-parameter tractable when parameterized below a natural bound. In addition, for the first parameterization we show that a kernel with O(k) vertices can be found in polynomial time.
Joint work with László Kozma and Jesper Nederlof
78. Computing the Chromatic Number Using Graph Decompositions via Matrix Rank
January 21st 2019, Dagstuhl, Germany
Computing the smallest number q such that the vertices of a given graph can be properly q-colored is one of the oldest and most fundamental problems in combinatorial optimization. The q-Coloring problem has been studied intensively using the framework of parameterized algorithmics, resulting in a very good understanding of the best-possible algorithms for several parameterizations based on the structure of the graph. For example, algorithms are known to solve the problem on graphs of treewidth tw in time O^*(q^tw), while a running time of O^*((q-epsilon)^tw) is impossible assuming the Strong Exponential Time Hypothesis (SETH). While there is an abundance of work for parameterizations based on decompositions of the graph by vertex separators, almost nothing is known about parameterizations based on edge separators. We fill this gap by studying q-Coloring parameterized by cutwidth, and parameterized by pathwidth in bounded-degree graphs. Our research uncovers interesting new ways to exploit small edge separators.
We present two algorithms for q-Coloring parameterized by cutwidth cutw: a deterministic one that runs in time O^*(2^(omega * cutw)), where omega is the matrix multiplication constant, and a randomized one with runtime O^*(2^cutw). In sharp contrast to earlier work, the running time is independent of q. The dependence on cutwidth is optimal: we prove that even 3-Coloring cannot be solved in O^*((2-epsilon)^cutw) time assuming SETH. Our algorithms rely on a new rank bound for a matrix that describes compatible colorings. Combined with a simple communication protocol for evaluating a product of two polynomials, this also yields an O^*((floor(d/2)+1)^pw) time randomized algorithm for q-Coloring on graphs of pathwidth pw and maximum degree d. Such a runtime was first obtained by Bjorklund, but only for graphs with few proper colorings. We also prove that this result is optimal in the sense that no O^*((floor(d/2)+1-epsilon)^pw)-time algorithm exists assuming SETH.
77. Gems in kernelization
November 28th 2018, Amsterdam, The Netherlands
When solving a hard computational problem, the running time can often be reduced by using a preprocessing step that throws away irrelevant parts of the data which are guaranteed not to affect the final answer. For a long time, there was no good explanation for the effectiveness of preprocessing. This changed when the notion of kernelization was developed within the field of parameterized complexity. It has been called ''the lost continent of polynomial time'', since the exploration of the formal model of preprocessing captured by kernelization has led to a surprisingly rich set of techniques that can reduce the size of NP-hard problem inputs in polynomial time, without changing the answer. Using a complexity-parameter, one can also give theoretical guarantees on the amount of data reduction that is achieved. This talk gives an introduction to kernelization by showcasing some of the gems of the area: elegant preprocessing schemes built on nontrivial mathematical insights. The presented gems deal with Edge Clique Cover, Vertex Cover, and Graph Coloring.
76. Computing the Chromatic Number Using Graph Decompositions via Matrix Rank
October 31st 2018, Asperen, The Netherlands
Computing the smallest number q such that the vertices of a given graph can be properly q-colored is one of the oldest and most fundamental problems in combinatorial optimization. The q-Coloring problem has been studied intensively using the framework of parameterized algorithmics, resulting in a very good understanding of the best-possible algorithms for several parameterizations based on the structure of the graph. For example, algorithms are known to solve the problem on graphs of treewidth tw in time O^*(q^tw), while a running time of O^*((q-epsilon)^tw) is impossible assuming the Strong Exponential Time Hypothesis (SETH). While there is an abundance of work for parameterizations based on decompositions of the graph by vertex separators, almost nothing is known about parameterizations based on edge separators. We fill this gap by studying q-Coloring parameterized by cutwidth. Our research uncovers interesting new ways to exploit small edge separators.
We present two algorithms for q-Coloring parameterized by cutwidth cutw: a deterministic one that runs in time O^*(2^(omega * cutw)), where omega is the matrix multiplication constant, and a randomized one with runtime O^*(2^cutw). In sharp contrast to earlier work, the running time is independent of q. The dependence on cutwidth is optimal: we prove that even 3-Coloring cannot be solved in O^*((2-epsilon)^cutw) time assuming SETH. Our algorithms rely on a new rank bound for a matrix that describes compatible colorings.
75. Lower Bounds for Dynamic Programming on Planar Graphs of Bounded Cutwidth
September 14th 2018, Eindhoven, Netherlands
Many combinatorial problems can be solved in time O^*(c^{tw}) on graphs of treewidth tw, for a problem-specific constant c. In several cases, matching upper and lower bounds on c are known based on the Strong Exponential Time Hypothesis (SETH). In this paper we investigate the complexity of solving problems on graphs of bounded cutwidth, a graph parameter that takes larger values than treewidth. We strengthen earlier treewidth-based lower bounds to show that, assuming SETH, Independent Set cannot be solved in O^*((2-epsilon)^{cutw}) time, and Dominating Set cannot be solved in O^*((3-epsilon)^{cutw}) time. By designing a new crossover gadget, we extend these lower bounds even to planar graphs of bounded cutwidth or treewidth. Hence planarity does not help when solving Independent Set or Dominating Set on graphs of bounded width. This sharply contrasts the fact that in many settings, planarity allows problems to be solved much more efficiently.
74. Best-case and Worst-case Sparsifiability of Boolean CSPs
August 23rd 2018, Helsinki, Finland
We continue the investigation of polynomial-time sparsification for NP-complete Boolean Constraint Satisfaction Problems (CSPs). The goal in sparsification is to reduce the number of constraints in a problem instance without changing the answer, such that a bound on the number of resulting constraints can be given in terms of the number of variables $n$. We investigate how the worst-case sparsification size depends on the types of constraints allowed in the problem formulation (the constraint language). Two algorithmic results are presented. The first result essentially shows that for any arity $k$, the only constraint type (up to negations) for which no nontrivial sparsification is possible, is the logical OR. Our second result concerns linear sparsification, i.e., a reduction to an equivalent instance with $Oh(n)$ constraints. Using linear algebra over rings of integers modulo prime powers, we give an elegant necessary and sufficient condition for a constraint type to be captured by a degree-$1$ polynomial over such a structure, which yields linear sparsifications. The combination of these algorithmic results allows us to prove two characterizations that capture the optimal sparsification sizes for a range of Boolean CSPs. For NP-complete Boolean CSPs whose constraints are symmetric (the satisfaction depends only on the number of 1 values in the assignment, not on their positions), we give a complete characterization of which constraint languages allow for a linear sparsification. For Boolean CSPs in which every constraint has arity at most three, we characterize the optimal size of sparsifications in terms of the largest OR that can be expressed by the constraint language.
73. 3rd Parameterized Algorithms & Computational Experiments Challenge
August 22nd 2018, Helsinki, Finland
This talk was given at the award ceremony of the 3rd Parameterized Algorithms & Computational Experiments Challenge (PACE 2018). The talk consists of several parts: where PACE came from (presented by me), how this year's Steiner Tree competition went (presented by Edouard Bonnet), a short talk by Daniel Rehfeldt, part of the winning team of Track B, and concludes with brief pointers about the next iteration. More information about PACE can be found on the website pacechallenge.wordpress.com. The third edition of PACE was sponsored by the Networks project and Data-Experts.de.
72. Lower Bounds for Dynamic Programming on Planar Graphs of Bounded Cutwidth
August 22nd 2018, Helsinki, Finland
Many combinatorial problems can be solved in time O^*(c^{tw}) on graphs of treewidth tw, for a problem-specific constant c. In several cases, matching upper and lower bounds on c are known based on the Strong Exponential Time Hypothesis (SETH). In this paper we investigate the complexity of solving problems on graphs of bounded cutwidth, a graph parameter that takes larger values than treewidth. We strengthen earlier treewidth-based lower bounds to show that, assuming SETH, Independent Set cannot be solved in O^*((2-epsilon)^{cutw}) time, and Dominating Set cannot be solved in O^*((3-epsilon)^{cutw}) time. By designing a new crossover gadget, we extend these lower bounds even to planar graphs of bounded cutwidth or treewidth. Hence planarity does not help when solving Independent Set or Dominating Set on graphs of bounded width. This sharply contrasts the fact that in many settings, planarity allows problems to be solved much more efficiently.
71. Computing the Chromatic Number Using Graph Decompositions via Matrix Rank
August 21st 2018, Helsinki, Finland
Computing the smallest number q such that the vertices of a given graph can be properly q-colored is one of the oldest and most fundamental problems in combinatorial optimization. The q-Coloring problem has been studied intensively using the framework of parameterized algorithmics, resulting in a very good understanding of the best-possible algorithms for several parameterizations based on the structure of the graph. For example, algorithms are known to solve the problem on graphs of treewidth tw in time O^*(q^tw), while a running time of O^*((q-epsilon)^tw) is impossible assuming the Strong Exponential Time Hypothesis (SETH). While there is an abundance of work for parameterizations based on decompositions of the graph by vertex separators, almost nothing is known about parameterizations based on edge separators. We fill this gap by studying q-Coloring parameterized by cutwidth, and parameterized by pathwidth in bounded-degree graphs. Our research uncovers interesting new ways to exploit small edge separators.
We present two algorithms for q-Coloring parameterized by cutwidth cutw: a deterministic one that runs in time O^*(2^(omega * cutw)), where omega is the matrix multiplication constant, and a randomized one with runtime O^*(2^cutw). In sharp contrast to earlier work, the running time is independent of q. The dependence on cutwidth is optimal: we prove that even 3-Coloring cannot be solved in O^*((2-epsilon)^cutw) time assuming SETH. Our algorithms rely on a new rank bound for a matrix that describes compatible colorings. Combined with a simple communication protocol for evaluating a product of two polynomials, this also yields an O^*((floor(d/2)+1)^pw) time randomized algorithm for q-Coloring on graphs of pathwidth pw and maximum degree d. Such a runtime was first obtained by Bjorklund, but only for graphs with few proper colorings. We also prove that this result is optimal in the sense that no O^*((floor(d/2)+1-epsilon)^pw)-time algorithm exists assuming SETH.
70. Polynomial Kernels for Hitting Forbidden Minors under Structural Parameterizations
August 21st 2018, Helsinki, Finland
We investigate polynomial-time preprocessing for the problem of hitting forbidden minors in a graph, using the framework of kernelization. For a fixed finite set of connected graphs F, the F-Deletion problem is the following: given a graph G and integer k, is it possible to delete k vertices from G to ensure the resulting graph does not contain any graph from F as a minor? Earlier work by Fomin, Lokshtanov, Misra, and Saurabh [FOCS'12] showed that when F contains a planar graph, an instance (G,k) can be reduced in polynomial time to an equivalent one of size k^{O(1)}. In this work we focus on structural measures of the complexity of an instance, with the aim of giving nontrivial preprocessing guarantees for instances whose solutions are large. Motivated by several impossibility results, we parameterize the F-Deletion problem by the size of a vertex modulator whose removal results in a graph of constant treedepth eta.
We prove that for each set F of connected graphs and constant eta, the F-Deletion problem parameterized by the size of a treedepth-eta modulator has a polynomial kernel. Our kernelization is fully explicit and does not depend on protrusion reduction or well-quasi-ordering, which are sources of algorithmic non-constructivity in earlier works on F-Deletion. Our main technical contribution is to analyze how models of a forbidden minor in a graph G with modulator X, interact with the various connected components of G-X. Using the language of labeled minors, we analyze the fragments of potential forbidden minor models that can remain after removing an optimal F-Deletion solution from a single connected component of G-X. By bounding the number of different types of behavior that can occur by a polynomial in |X|, we obtain a polynomial kernel using a recursive preprocessing strategy. Our results extend earlier work for specific instances of F-Deletion such as Vertex Cover and Feedback Vertex Set. It also generalizes earlier preprocessing results for F-Deletion parameterized by a vertex cover, which is a treedepth-one modulator.
69. Gems in Kernelization
July 12th 2018, Dagstuhl, Germany
When solving a hard computational problem, the running time can often be reduced by using a preprocessing step that throws away irrelevant parts of the data which are guaranteed not to affect the final answer. Until recently, there was no good explanation for the effectiveness of preprocessing. This changed when the notion of kernelization was developed within the field of parameterized complexity. It has been called ''the lost continent of polynomial time'', since the exploration of the formal model of preprocessing captured by kernelization has led to a surprisingly rich set of techniques that can reduce the size of NP-hard problem inputs in polynomial time, without changing the answer. Using a user-defined complexity-parameter, one can also give theoretical guarantees on the amount of data reduction that is achieved. This talk gives an introduction to kernelization by showcasing some of the gems of the area: elegant preprocessing schemes built on nontrivial mathematical insights. The presented gems deal with Edge Clique Cover, Vertex Cover, and Graph Coloring.
68. Introduction to Parameterized Algorithms
July 9th 2018, Dagstuhl, Germany
This tutorial introduces the main concepts in fixed-parameter tractability. It treats both the positive toolkit (techniques for algorithms) and the negative toolkit (techniques for hardness proofs). Examples from the positive toolkit include bounded-depth search trees, kernelization, color coding, and treewidth-based dynamic programming. When it comes to hardness proofs it covers W[1]-hardness and some kernelization lower bounds.
67. Polynomial Kernels for Hitting Forbidden Minors under Structural Parameterizations
October 9th 2017, Warsaw, Poland
We investigate polynomial-time preprocessing for the problem of hitting forbidden minors in a graph, using the framework of kernelization. For a fixed finite set of connected graphs F, the F-Deletion problem is the following: given a graph G and integer k, is it possible to delete k vertices from G to ensure the resulting graph does not contain any graph from F as a minor? Earlier work [Fomin et al. FOCS'12] showed that when F contains a planar graph, an instance (G,k) can be reduced in polynomial time to an equivalent one of size k^O(1). In this work we focus on structural measures of the complexity of an instance, with the aim of giving nontrivial preprocessing guarantees for instances whose solutions are large. Motivated by several impossibility results, we parameterize the F-Deletion problem by the size of a vertex modulator whose removal results in a graph of constant treedepth \eta. We prove that for every choice of F and \eta, the F-Deletion problem parameterized by the size of a treedepth-\eta modulator has a polynomial kernel. Our kernelization is fully explicit and does not depend on protrusion reduction or well-quasi-ordering, which are sources of algorithmic non-constructivity in earlier works on F-Deletion. Our main technical contribution is to analyze how models of a forbidden minor in a graph G with modulator X, interact with the various connected components of G-X. Using the language of labeled minors, we analyze the fragments of potential forbidden minor models that can remain after removing an optimal F-Deletion solution from a single connected component of G-X. By bounding the number of different types of behavior that can occur by a polynomial in |X|, we obtain a polynomial kernel using a recursive preprocessing strategy. Our results extend earlier work for specific instances of F-Deletion such as Vertex Cover and Feedback Vertex Set. It also generalizes earlier preprocessing results for F-Deletion parameterized by a vertex cover, which is a treedepth-one modulator. Joint work with Astrid Pieterse.
66. Fine-Grained Complexity Analysis of Improving Traveling Salesman Tours
October 31st 2017, Asperen, The Netherlands
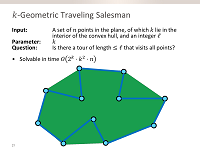
We analyze the complexity of finding k-OPT improvements to a given traveling salesman tour, using the toolkit of fine-grained complexity. The problem can be solved in O(n^k) time for each k. We give evidence that this is optimal for k=3 using the APSP-conjecture. For larger k, we give a new algorithm that finds the best k-move in O(n^{floor{2k/3} + 1). Joint work with Mark de Berg, Kevin Buchin, and Gerhard Woeginger.
65. 2nd Parameterized Algorithms & Computational Experiments Challenge
September 6th 2017, Vienna, Austria
This talk was given at the award ceremony of the 2nd Parameterized Algorithms & Computational Experiments Challenge (PACE 2017). The talk consists of several parts: where PACE came from (presented by me), how track A went (presented by Holger Dell), a short talk by the winning team of the exact subcompetition of track A (Felix Salfelder), how track B went (presented by Christian Komusiewicz), and a short talk by the winning team of track B (Yasuaki Kobayashi). More information about PACE can be found on the website pacechallenge.wordpress.com. The second edition of PACE was sponsored by the Networks project.
64. Kernelization Basics:
Exploring the Lost Continent of Polynomial Time
September 2nd 2017, Vienna, Austria
Join me on a tour through the lost continent of polynomial-time computation, where we find provably efficient and provably effective preprocessing algorithms to attack NP-hard problems. The talk introduces the concept of kernelization and showcases several fundamental ideas such as crown decompositions and the sunflower lemma. These are applied to obtain kernels for Edge Clique Cover, Vertex Cover, and Hitting Set.
63. Gems in (the vocabulary of) Multivariate Algorithmics:
A tribute to Mike Fellows
June 16th 2017, Bergen, Norway
Mike Fellows has contributed many ideas, techniques, and problems to the field of multivariate algorithmics. But his influence is also strongly felt through the vocabulary we use! I reflect on my history with Mike based on some of the colorful terminology he introduced, while describing old and new results along the way.
62. Fine-Grained Complexity Analysis of Two Classic TSP Variants
June 11th 2017, Berlin, Germany
We analyze two classic variants of the Traveling Salesman Problem using the toolkit of fine-grained complexity. The first variant we consider is the Bitonic TSP problem: given a set of n points in the plane, compute a shortest tour consisting of two x-monotone chains. It is a classic exercise to solve this problem in O(n^2) time. We show that this is far from optimal: bitonic tours can be found in O(n log^2 n) time. The second variant is the k-OPT decision problem, which asks whether a given tour can be improved by replacing k edges. The problem can be solved in O(n^k) time for each k. We give evidence that this is optimal for k=3 using the APSP-conjecture. For larger k, we give a new algorithm that finds the best k-move in O(n^{floor{2k/3} + 1). Joint work with Mark de Berg, Kevin Buchin, and Gerhard Woeginger.
61. Micro-course on Structural Graph Parameters, part 3:
Applications
February 2nd 2017, Doorn, The Netherlands
This microcourse deals with structural graph parameters and the relations between them. A graph parameter assigns a number to a graph, by answering a question such as 'how many edges are there?', 'how many vertices are needed to intersect all the cycles?', or 'what is the size of the largest clique?'. Over the last decades, the study of structural graph theory has produced a rich toolbox of different graph parameters that also capture more subtle aspects of the structure of a graph. For example, the parameter treewidth gives a formal way to answer the question: 'how treelike is this graph?'. The goal of the microcourse is to introduce useful graph parameters and relate them to each other. The hierarchy among graph parameters facilitates a research methodology that has proven very useful: start by exploring the research question of interest on graphs that are structurally simple according to a 'very restrictive' parameter, and repeatedly generalize the resulting insights to more and more general parameters. The concepts of structural graph theory also find applications in parameterized computational complexity. When faced with a computational problem that is intractable (NP-complete) in general, one can study whether it can be solved efficiently on large graphs that are structurally simple in terms of a chosen parameter. Investigating how the computational complexity of the problem depends on the value of a structural parameter results in an extended dialogue with a computational problem that yields important insights in the types of inputs for which it can be solved efficiently. If time permits, we will explore some examples of the application of structural graph theory to parameterized complexity.
60. Micro-course on Structural Graph Parameters, part 2:
A hierarchy of graph parameters
February 1st 2017, Doorn, The Netherlands
This microcourse deals with structural graph parameters and the relations between them. A graph parameter assigns a number to a graph, by answering a question such as 'how many edges are there?', 'how many vertices are needed to intersect all the cycles?', or 'what is the size of the largest clique?'. Over the last decades, the study of structural graph theory has produced a rich toolbox of different graph parameters that also capture more subtle aspects of the structure of a graph. For example, the parameter treewidth gives a formal way to answer the question: 'how treelike is this graph?'. The goal of the microcourse is to introduce useful graph parameters and relate them to each other. The hierarchy among graph parameters facilitates a research methodology that has proven very useful: start by exploring the research question of interest on graphs that are structurally simple according to a 'very restrictive' parameter, and repeatedly generalize the resulting insights to more and more general parameters. The concepts of structural graph theory also find applications in parameterized computational complexity. When faced with a computational problem that is intractable (NP-complete) in general, one can study whether it can be solved efficiently on large graphs that are structurally simple in terms of a chosen parameter. Investigating how the computational complexity of the problem depends on the value of a structural parameter results in an extended dialogue with a computational problem that yields important insights in the types of inputs for which it can be solved efficiently. If time permits, we will explore some examples of the application of structural graph theory to parameterized complexity.
59. Micro-course on Structural Graph Parameters, part 1:
Treewidth
January 31st 2017, Doorn, The Netherlands
This microcourse deals with structural graph parameters and the relations between them. A graph parameter assigns a number to a graph, by answering a question such as 'how many edges are there?', 'how many vertices are needed to intersect all the cycles?', or 'what is the size of the largest clique?'. Over the last decades, the study of structural graph theory has produced a rich toolbox of different graph parameters that also capture more subtle aspects of the structure of a graph. For example, the parameter treewidth gives a formal way to answer the question: 'how treelike is this graph?'. The goal of the microcourse is to introduce useful graph parameters and relate them to each other. The hierarchy among graph parameters facilitates a research methodology that has proven very useful: start by exploring the research question of interest on graphs that are structurally simple according to a 'very restrictive' parameter, and repeatedly generalize the resulting insights to more and more general parameters. The concepts of structural graph theory also find applications in parameterized computational complexity. When faced with a computational problem that is intractable (NP-complete) in general, one can study whether it can be solved efficiently on large graphs that are structurally simple in terms of a chosen parameter. Investigating how the computational complexity of the problem depends on the value of a structural parameter results in an extended dialogue with a computational problem that yields important insights in the types of inputs for which it can be solved efficiently. If time permits, we will explore some examples of the application of structural graph theory to parameterized complexity.
58. Approximation and Kernelization for Chordal Vertex Deletion
January 18th 2017, Barcelona, Spain
The Chordal Vertex Deletion (ChVD) problem asks to delete a minimum number of vertices from an input graph to obtain a chordal graph. In this paper we develop a polynomial kernel for ChVD under the parameterization by the solution size. Using a new Erdos-Posa type packing/covering duality for holes in nearly-chordal graphs, we present a polynomial-time algorithm that reduces any instance (G,k) of ChVD to an equivalent instance with poly(k) vertices. The existence of a polynomial kernel answers an open problem of Marx from 2006 [WG 2006, LNCS 4271, 37--48]. To obtain the kernelization, we develop the first poly(opt)-approximation algorithm for ChVD, which is of independent interest. In polynomial time, it either decides that G has no chordal deletion set of size k, or outputs a solution of size O(k^4 \log^2 k).
57. The Power of Preprocessing:
Gems in Kernelization
Combinatorial Optimization meets Parameterized Complexity [Invited talk]
December 13th 2016, Bonn, Germany
When solving a hard computational problem, the running time can often be reduced by using a preprocessing step that throws away irrelevant parts of the data which are guaranteed not to affect the final answer. Until recently, there was no good explanation for the effectiveness of preprocessing. This changed when the notion of kernelization was developed within the field of parameterized complexity. It has been called ''the lost continent of polynomial time'', since the exploration of the formal model of preprocessing captured by kernelization has led to a surprisingly rich set of techniques that can reduce the size of NP-hard problem inputs in polynomial time, without changing the answer. Using a user-defined complexity-parameter, one can also give theoretical guarantees on the amount of data reduction that is achieved. This talk gives an introduction to kernelization by showcasing some of the gems of the area: elegant preprocessing schemes built on nontrivial mathematical insights. One of the gems consists of a polynomial kernelization for the undirected Feedback Vertex Set problem. While the existence of a kernel is not new, the presented approach and its elegant correctness proof were not known before.
56. A treasure found on the lost continent of polynomial time:
Kernelization for Feedback Vertex Set
December 6th 2016, Eindhoven, The Netherlands
When solving a hard computational problem, the running time can often be reduced by using a preprocessing step that throws away irrelevant parts of the data which are guaranteed not to affect the final answer. Until recently, there was no good explanation for the effectiveness of preprocessing. This changed when the notion of kernelization was developed within the field of parameterized complexity. It has been called ''the lost continent of polynomial time'', since the exploration of the formal model of preprocessing captured by kernelization has led to a surprisingly rich set of techniques that can reduce the size of NP-hard problem inputs in polynomial time, without changing the answer. Using a user-defined complexity-parameter, one can also give theoretical guarantees on the amount of data reduction that is achieved. This talk presents a modern exposition of one of the treasures that has been found on the lost continent: an efficient and provably effective preprocessing algorithm for the undirected Feedback Vertex Set problem (FVS), which asks to find a minimum vertex set whose removal makes the graph acyclic. While kernelization algorithms for FVS are not new, the presented approach and its elegant correctness proof were not known before.
55. Optimal Sparsification for Some Binary CSPs Using Low-Degree Polynomials
October 14th 2016, Bergen, Norway
This talk investigates to what extent it is possible to efficiently reduce the number of clauses in NP-hard satisfiability problems, without changing the answer. Upper and lower bounds are established using the concept of kernelization. Existing results show that if NP is not contained in coNP/poly, no efficient preprocessing algorithm can reduce n-variable instances of CNF-SAT with d literals per clause, to equivalent instances with O(n^{d-epsilon}) bits for any epsilon > 0. For the Not-All-Equal SAT problem, a compression to size tilde-O(n^{d-1}) exists. We put these results in a common framework by analyzing the compressibility of binary CSPs. We characterize constraint types based on the minimum degree of multivariate polynomials whose roots correspond to the satisfying assignments, obtaining (nearly) matching upper and lower bounds in several settings. Our lower bounds show that not just the number of constraints, but also the encoding size of individual constraints plays an important role. For example, for Exact Satisfiability with unbounded clause length it is possible to efficiently reduce the number of constraints to n+1, yet no polynomial-time algorithm can reduce to an equivalent instance with O(n^{2-epsilon}) bits for any epsilon > 0, unless NP is contained in coNP/poly.
54. 1st Parameterized Algorithms & Computational Experiments Challenge
August 24th 2016, Aarhus, Denmark
This talk was given at the award ceremony of the 1st Parameterized Algorithms & Computational Experiments Challenge (PACE 2016). The talk consists of four parts: where PACE came from (presented by me), how track A went (presented by Holger Dell), how track B went (presented by Christian Komusiewicz), and what will happen for PACE in the future (again presented by me). More information about PACE can be found on the website pacechallenge.wordpress.com. The first edition of PACE was sponsored by the Networks project.
53. Fine-Grained Complexity Analysis of Two Classic TSP Variants
July 12th 2016, Rome, Italy
We analyze two classic variants of the Traveling Salesman Problem using the toolkit of fine-grained complexity. The first variant we consider is the Bitonic TSP problem: given a set of n points in the plane, compute a shortest tour consisting of two x-monotone chains. It is a classic exercise to solve this problem in O(n^2) time. We show that this is far from optimal: bitonic tours can be found in O(n log^2 n) time. The second variant is the k-OPT decision problem, which asks whether a given tour can be improved by replacing k edges. The problem can be solved in O(n^k) time for each k. We give evidence that this is optimal for k=3 using the APSP-conjecture. For larger k, we give a new algorithm that finds the best k-move in O(n^{floor{2k/3} + 1). Joint work with Mark de Berg, Kevin Buchin, and Gerhard Woeginger.
52. Turing Kernelization for Finding Long Paths and Cycles in Planar Graphs
June 3rd 2016, Dagstuhl, Germany
The k-Path problem asks whether a given undirected graph has a (simple) path of length k. We prove that k-Path has polynomial-size Turing kernels when restricted to planar graphs, graphs of bounded degree, claw-free graphs, or to K_{3,t}-minor-free graphs. This means that there is an algorithm that, given a k-Path instance (G,k) belonging to one of these graph classes, computes its answer in polynomial time when given access to an oracle that solves k-Path instances of size polynomial in k in a single step. Our techniques also apply to k-Cycle, which asks for a cycle of length at least k.
51. Introduction to Fixed-Parameter Tractability
with links to Computational Geometry
April 4th 2016, Leiden, Netherlands
This tutorial introduces the main concepts in fixed-parameter tractability to an audience with a background in computational geometry. It treats both the positive toolkit (techniques for algorithms) and the negative toolkit (techniques for hardness proofs). Examples from the positive toolkit include bounded-depth search trees, kernelization, and color coding. When it comes to hardness proofs it covers W[1]-hardness and the (strong) exponential time hypothesis.
50. Fine-grained Complexity Analysis of Computational Problems on Networks
March 23rd 2016, Amsterdam, Netherlands
This talk gives an introduction to fine-grained complexity analysis, which classifies the computational complexity of problems on a finer scale than the traditional distinction between polynomial-time solvable and NP-complete problems. In recent years there have been tremendous advances in our understanding of the best-possible running time to solve classic problems on networks such as finding (all-pairs) shortest paths and detecting triangles. These new developments are based on new hypotheses about the running time of fundamental optimization problems, together with a web of intricate reductions relating the complexities of various problems to each other. The goal of the presentation is to give an accessible overview of some key results in this area concerning networks, and to give examples of the reductions that are used. For example, we will see that from the right perspective the problem of computing all pairs of shortest path distances in a graph is equivalent to the problem of finding a triangle whose sum of edge weights is negative.
49. Constrained Bipartite Vertex Cover: The Easy Kernel is Essentially Tight
February 18th 2016, Orléans, France
The Constrained Bipartite Vertex Cover problem asks, for a bipartite graph G with partite sets A and B, and integers k_A and k_B, whether there is a vertex cover for G containing at most k_A vertices from A and k_B vertices from B. The problem has an easy kernel with 2 k_A * k_B edges and 4 k_A * k_B vertices, based on the fact that every vertex in A of degree more than k_B has to be included in the solution, together with every vertex in B of degree more than k_A. We prove that this kernel is asymptotically essentially optimal, both in terms of the number of vertices and the number of edges. We prove that if there is a polynomial-time algorithm that reduces any instance (G,A,B,k_A,k_B) of Constrained Bipartite Vertex Cover to an equivalent instance (G',A',B',k'_A,k'_A) such that k'_A <= (k_A)^O(1), k'_B <= (k_B)^O(1), and |V(G')| <= O((k_A * k_B)^{1 - \eps}), for any \eps > 0, then NP is in coNP/poly and the polynomial-time hierarchy collapses. Using a different construction, we prove that if there is a polynomial-time algorithm that reduces any instance to an equivalent instance with O((k_A * k_B)^{1 - \eps}) edges, then NP is in coNP/poly.
48. Fine-grained Complexity and Algorithm Design
November 10th 2015, Eindhoven, The Netherlands
During the fall semester of 2015, the Simons institute in Berkeley hosted a research program on "fine-grained complexity and algorithm design". In this informal talk I will describe what the program was about and mention some remarkable recent results in this area. In particular, I will show how elementary reductions can establish the equivalence of a class of fundamental combinatorial problems with respect to having "truly subcubic" algorithms, even though these problems seem to behave very differently at first sight.
47. Fine-Grained Complexity Analysis of Two Classic TSP Variants
October 27th 2015, Berkeley, USA
We analyze two classic variants of the Traveling Salesman Problem using the toolkit of fine-grained complexity. The first variant we consider is the Bitonic TSP problem: given a set of n points in the plane, compute a shortest tour consisting of two x-monotone chains. It is a classic exercise to solve this problem in O(n^2) time. We show that this is far from optimal: bitonic tours can be found in O(n log^2 n) time. The second variant is the k-OPT decision problem, which asks whether a given tour can be improved by replacing k edges. The problem can be solved in O(n^k) time for each k. We give evidence that this is optimal for k=3 using the APSP-conjecture. For larger k, we give a new algorithm that finds the best k-move in O(n^{floor{2k/3} + 1). Joint work with Mark de Berg, Kevin Buchin, and Gerhard Woeginger.
46. Fine-Grained Complexity Analysis of Two Classic TSP Variants
July 28th 2015, Eindhoven, The Netherlands
This informal board talk presented joint work with Mark de Berg, Kevin Buchin, and Gerhard Woeginger, on new results concerning two classic TSP variants. We prove that the O(n^2)-time dynamic program for finding Bitonic TSP tours among points in the plane, can be improved to O(n log^2 n). We also analyze the complexity of finding a k-OPT improvement to a given TSP tour, which is a subproblem occurring when using local search approaches for TSP. We show that the best 2-OPT and 3-OPT improvements can be found in O(n^2) and O(n^3) time, respectively, and give evidence that this is optimal. For larger k, we show that the best k-OPT move can be found in O(n^floor(2k/3)+1) time.
45. Uniform Kernelization Complexity of Hitting Forbidden Minors
July 8th 2015, Kyoto, Japan
The F-Minor-Free Deletion problem asks, for a fixed set F and an input consisting of a graph G and integer k, whether k vertices can be removed from G such that the resulting graph does not contain any member of F as a minor. This paper analyzes to what extent provably effective and efficient preprocessing is possible for F-Minor-Free Deletion. Fomin et al. (FOCS 2012) showed that the special case Planar F-Deletion (when F contains at least one planar graph) has a kernel of size f(F) * k^{g(F)} for some functions f and g. The degree g of the polynomial grows very quickly; it is not even known to be computable. Fomin et al. left open whether Planar F-Deletion has kernels whose size is uniformly polynomial, i.e., of the form f(F) * k^c for some universal constant c that does not depend on F. Our results in this paper are twofold. (1) We prove that some Planar F-Deletion problems do not have uniformly polynomial kernels (unless NP is in coNP/poly). In particular, we prove that Treewidth-Eta Deletion does not have a kernel with O(k^{eta/4} - eps) vertices for any eps > 0, unless NP is in coNP/poly. In fact, we even prove the kernelization lower bound for the larger parameter vertex cover number. This resolves an open problem of Cygan et al. (IPEC 2011). It is a natural question whether further restrictions on F lead to uniformly polynomial kernels. However, we prove that even when F contains a path, the degree of the polynomial must, in general, depend on the set F. (2) A canonical F-Minor-Free Deletion problem when F contains a path is Treedepth-eta Deletion: can k vertices be removed to obtain a graph of treedepth at most eta? We prove that Treedepth-eta Deletion admits uniformly polynomial kernels with O(k^6) vertices for every fixed eta. In order to develop the kernelization we prove several new results about the structure of optimal treedepth-decompositions. These insights allow us to formulate a simple, fully explicit, algorithm to reduce the instance.
44. On Structural Parameterizations of Hitting Set:
Hitting Paths in Graphs Using 2-SAT
June 19th 2015, Münich, Germany
Hitting Set is a classic problem in combinatorial optimization. Its input consists of a set system F over a finite universe U and an integer t; the question is whether there is a set of t elements that intersects every set in F. The Hitting Set problem parameterized by the size of the solution is a well-known W[2]-complete problem in parameterized complexity theory. In this paper we investigate the complexity of Hitting Set under various structural parameterizations of the input. Our starting point is the folklore result that Hitting Set is polynomial-time solvable if there is a tree T on vertex set U such that the sets in F induce connected subtrees of T. We consider the case that there is a treelike graph with vertex set U such that the sets in F induce connected subgraphs; the parameter of the problem is a measure of how treelike the graph is. Our main positive result is an algorithm that, given a graph G with cyclomatic number k, a collection P of simple paths in G, and an integer t, determines in time 2^{5k} (|G| +|P|)^O(1) whether there is a vertex set of size t that hits all paths in P. It is based on a connection to the 2-SAT problem in multiple valued logic. For other parameterizations we derive W[1]-hardness and para-NP-completeness results.
43. Constrained Bipartite Vertex Cover: The Easy Kernel is Essentially Tight
June 4th 2015, Nordfjordeid, Norway
The Constrained Bipartite Vertex Cover problem asks, for a bipartite graph G with partite sets A and B, and integers k_A and k_B, whether there is a vertex cover for G containing at most k_A vertices from A and k_B vertices from B. The problem has an easy kernel with 2 k_A * k_B edges and 4 k_A * k_B vertices, based on the fact that every vertex in A of degree more than k_B has to be included in the solution, together with every vertex in B of degree more than k_A. We prove that this kernel is asymptotically essentially optimal, both in terms of the number of vertices and the number of edges. We prove that if there is a polynomial-time algorithm that reduces any instance (G,A,B,k_A,k_B) of Constrained Bipartite Vertex Cover to an equivalent instance (G',A',B',k'_A,k'_A) such that k'_A <= (k_A)^O(1), k'_B <= (k_B)^O(1), and |V(G')| <= (k_A * k_B)^(1 - eps), for any eps > 0, then NP is in coNP/poly and the polynomial-time hierarchy collapses. Using a different construction, we prove that if there is a polynomial-time algorithm that reduces any instance to an equivalent instance with O((k_A * k_B)^(1 - eps) edges, then NP is in coNP/poly.
42. Turing Kernelization for Finding Long Paths
and Cycles in Restricted Graph Classes
June 3rd 2015, Nordfjordeid, Norway
We present a set of results concerning the existence of polynomial-size Turing kernels for the problems of finding long simple paths and cycles in restricted graph families such as planar graphs, bounded-degree graphs, and claw-free graphs. The adaptive Turing kernelization works on the Tutte decomposition of the graph into triconnected components. Existing graph-theoretical lower bounds on the length of long paths in triconnected graphs allow us to answer YES if the Tutte decomposition has a bag of size superpolynomial in k. If this is not the case, we can identify a vertex that is irrelevant to the solution in polynomial time by querying an oracle for long paths or cycles in leaf components of the decomposition. The number of vertices involved in these queries is therefore polynomial in k, resulting in polynomial-size Turing kernels. The employed method is called Decompose-Query-Reduce and is potentially useful for other problems. Our Turing kernel shows that on these restricted graph classes, the hard part of the computation for finding a length-k path or cycle can be restricted to graphs whose size is polynomial in k.
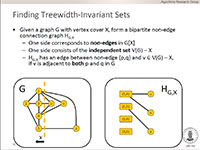
41. On Sparsification for Computing Treewidth
March 16th 2015, Eindhoven, The Netherlands
We study whether an n-vertex instance (G,k) of Treewidth, asking whether the graph G has treewidth at most k, can efficiently be made sparse without changing its answer. By giving a special form of OR-cross-composition, we prove that this is not the case: if there is an e>0 and a polynomial-time algorithm that reduces n-vertex Treewidth instances to equivalent instances, of an arbitrary problem, with O(n^{2-e}) bits, then NP is in coNP/poly and the polynomial hierarchy collapses.
Our sparsification lower bound has implications for structural parameterizations of Treewidth: parameterizations by measures that do not exceed the vertex count, cannot have kernels with O(k^{2-e}) bits for any e>0, unless NP is in coNP/poly. Motivated by the question of determining the optimal kernel size for Treewidth parameterized by vertex cover, we improve the O(k^3)-vertex kernel from Bodlaender et al. (STACS 2011) to a kernel with O(k^2) vertices. Our improved kernel is based on a novel form of treewidth-invariant set. We use the q-expansion lemma of Fomin et al.(STACS 2011) to find such sets efficiently in graphs whose vertex count is superquadratic in their vertex cover number.
40. Characterizing the Easy-to-Find Subgraphs from the Viewpoint of Polynomial-Time Algorithms, Kernels, and Turing Kernels
January 16th 2015, Edinburgh, United Kingdom
We study two fundamental problems related to finding subgraphs: given graphs G and H, test whether H is isomorphic to a subgraph of G, or determine the maximum number of vertex-disjoint H-subgraphs that can be packed in G. We investigate these problems when the graph H belongs to a fixed hereditary family F. Our goal is to study which classes F make the two problems tractable in one of the following senses: (a) (randomized) polynomial-time solvable, (b) admits a polynomial (many-one) kernel, or (c) admits a polynomial Turing kernel. Joint work with Dániel Marx.
39. Characterizing the Easy-to-Find Subgraphs from the Viewpoint of Polynomial-Time Algorithms, Kernels, and Turing Kernels
January 4th 2015, San Diego, California, USA
We study two fundamental problems related to finding subgraphs: given graphs G and H, test whether H is isomorphic to a subgraph of G, or determine the maximum number of vertex-disjoint H-subgraphs that can be packed in G. We investigate these problems when the graph H belongs to a fixed hereditary family F. Our goal is to study which classes F make the two problems tractable in one of the following senses: (a) (randomized) polynomial-time solvable, (b) admits a polynomial (many-one) kernel, or (c) admits a polynomial Turing kernel. Joint work with Dániel Marx.
38. Uniform Kernelization Complexity of Hitting Forbidden Minors
November 5th 2014, Dagstuhl, Germany
Several results are known concerning the optimality of the sizes of problem kernels. For example, a result of Dell and van Melkebeek shows that k-Vertex Cover does not have a kernel with O(k^(2-epsilon)) bits, for any positive epsilon, unless NP is in coNP/poly. For other problems, we are much further from establishing the optimal kernel size. A large family of vertex deletion problems can be captured in the framework of F-Minor-free Deletion problems. For a fixed, finite family F, the F-Minor-free Deletion problem takes as input a graph G and an integer k, and asks whether k vertices can be removed from G such that the resulting graph does not contain any graph in F as a minor. This generalizes k-Vertex Cover, k-Feedback Vertex Set, k-Vertex Planarization, and other problems. A breakthrough result by Fomin et al. (FOCS 2012) shows that if F contains a planar graph (implying that F-minor-free graphs have constant treewidth), the F-Minor-Free deletion problem has a polynomial kernel. Concretely, there is a function g (which is not known to be computable) such that F-Minor-Free deletion has a kernel with O(k^(g(F))) vertices. As F-Minor-Free deletion captures a large number of classic problems, it would be desirable to find kernels of optimal size. A first question towards finding the optimal kernel size for such problems is whether F-Minor-Free deletion has kernels of uniformly polynomial size, i.e., of size g(F) * k^c for some constant c that does not depend on the family F. We show that this is not the case: assuming NP is not in coNP/poly, F-Minor-Free deletion does not have uniformly polynomial kernels. We can also prove the following contrasting, positive result: there is a function g such that, for every t, the Treedepth-t Deletion problem has a kernel with g(k) * k^c vertices for a small, absolute constant c. Since for every fixed t, the Treedepth-t deletion problem is an instance of F-Minor-Free deletion, this shows that when the family of forbidden minors enforce sufficient structure on the solution graphs, uniformly polynomial kernels can be obtained. Our results therefore form the first step into analyzing exactly which aspects of the family of forbidden minors determine the degree of the polynomial in the optimal kernel size. Joint work with Archontia Giannopoulou, Daniel Lokshtanov, and Saket Saurabh.
37. Parameterized Algorithmics
October 17th 2014, Amsterdam, The Netherlands
In this talk for the Networks project I try to bridge the gap between researchers working on algorithmics and researchers working on stochastics. I introduce the framework of parameterized algorithmics for the analysis of NP-hard problems, and suggest some problems on the interface of algorithmics and stochastics.
36. Pleased to meet you
October 16th 2014, Eindhoven, The Netherlands
35. Characterizing the Easy-to-Find Subgraphs from the Viewpoint of Polynomial-Time Algorithms, Kernels, and Turing Kernels
October 7th 2014, Saarbrücken, Germany
We study two fundamental problems related to finding subgraphs: given graphs G and H, test whether H is isomorphic to a subgraph of G, or determine the maximum number of vertex-disjoint H-subgraphs that can be packed in G. We investigate these problems when the graph H belongs to a fixed hereditary family F. Our goal is to study which classes F make the two problems tractable in one of the following senses: (a) (randomized) polynomial-time solvable, (b) admits a polynomial (many-one) kernel (that is, has a polynomial-time preprocessing procedure that creates an equivalent instance whose size is polynomially bounded by the size of the solution), or (c) admits a polynomial Turing kernel (that is, has an adaptive polynomial-time procedure that reduces the problem to a polynomial number of instances, each of which has size bounded polynomially by the size of the solution). In an informal board talk I will present the context for our investigations, the concrete results we obtained, and sketch some of the technical ideas that are involved. This is joint work with Daniel Marx and will be presented at SODA 2015 in January.
34. The Power of Preprocessing
September 29th 2014, Eindhoven, The Netherlands
I recently joined the Algorithms & Visualization group at the TU Eindhoven. Most of my work so far concerns provably effective and efficient preprocessing for NP-hard problems, which can be formalized using the language of parameterized complexity theory. In my first lecture here in Eindhoven I will give a gentle introduction into this field, highlighted by pointers to some of my recent work. I will introduce and motivate the basic notion of kernelization that captures good preprocessing. Afterward we will also consider some variations of this basic model. We conclude by considering a recent preprocessing algorithm for the Longest Path problem in more detail. I presented this algorithm at the European Symposium on Algorithms two weeks ago.
33. Turing Kernelization for Finding Long Paths
and Cycles in Restricted Graph Classes
September 8th 2014, Wrocław, Poland
We present a set of new results concerning the existence of polynomial-size Turing kernels for the problems of finding long simple paths and cycles in restricted graph families such as planar graphs, bounded-degree graphs, and claw-free graphs. The adaptive Turing kernelization works on the Tutte decomposition of the graph into triconnected components. Existing graph-theoretical lower bounds on the length of long paths in triconnected graphs allow us to answer YES if the Tutte decomposition has a bag of size superpolynomial in k. If this is not the case, we can identify a vertex that is irrelevant to the solution in polynomial time by querying an oracle for long paths or cycles in leaf components of the decomposition. The number of vertices involved in these queries is therefore polynomial in k, resulting in polynomial-size Turing kernels. The employed method is called Decompose-Query-Reduce and is potentially useful for other problems. Our Turing kernel shows that on these restricted graph classes, the hard part of the computation for finding a length-k path or cycle can be restricted to graphs whose size is polynomial in k.
32. Parameterized Algorithms: Advanced Kernelization Techniques
August 20th 2014, Będlewo, Poland
This is a lecture of the 2014 School on Parameterized Algorithms and Complexity that was held in Będlewo, Poland. The topic is advanced kernelation techniques. The lecture is roughly split in two parts. The first part shows how many problems become easier when restricted to planar graphs. A 4k-vertex kernel is developed for Connected Vertex Cover in planar graphs, while the problem does not admit a polynomial kernel in general graphs unless the polynomial-time hierarchy collapses. The second part of the lecture focuses on Turing kernelization. The simple example of the Max Leaf Subtree shows that Turing kernelization can be used to analyze meaningful preprocessing schemes for problems that do not have traditional kernels of small size. We conclude by considering the very recent Turing kernel for the Longest Path problem on planar graphs.
31. Parameterized Algorithms: Randomized Algorithms
August 18th 2014, Będlewo, Poland
This was the third lecture of the 2014 School on Parameterized Algorithms and Complexity that was held in Będlewo, Poland. It deals with randomized FPT algorithms, mostly using the color coding paradigm. Randomized FPT algorithms are presented for Longest Path, Subgraph Isomorphism on Bounded-Degree graphs, and d-Clustering. After briefly considering the derandomization issue, the lecture concludes with a simple randomized algorithm for Feedback Vertex Set.
30. Parameterized Algorithms: The Basics
August 18th 2014, Będlewo, Poland
This was the opening lecture of the 2014 School on Parameterized Algorithms and Complexity that was held in Będlewo, Poland. After briefly surveying the history of parameterized complexity, it starts by defining the basics concepts of parameterized tractability. Three types of parameterized algorithms are presented: kernelization algorithms (illustrated for Vertex Cover and Feedback Arc Set in Tournaments), bounded-depth search trees (illustrated for Vertex Cover and Feedback Vertex Set), and dynamic programming over subsets (illustrated for Set Cover).
29. The Power of Preprocessing
July 13th 2014, Eindhoven, The Netherlands
During this 20-minute talk I give an informal overview of some of my recent work concerning preprocessing, (Turing) kernelization, and parameterized algorithmics. The high-level ideas are conveyed through pictures, along with pointers to my research papers. Among the discussed papers are a recent result with Daniel Marx concerning preprocessing for finding patterns in large networks, the survey paper with Mike Fellows and Frances Rosamond suggesting a wide exploration of the parameter landscape, a paper on graph coloring with Stefan Kratsch, my recent paper on Turing kernelization for finding long paths in planar graphs, and a paper with Daniel Lokshtanov and Saket Saurabh concerning efficient parameterized algorithms for the planarization problem.
28. Turing Kernelization for Finding Long Paths
and Cycles in Restricted Graph Classes
May 9th 2014, Bergen, Norway
In this informal board talk we present a set of new results concerning the existence of polynomial-size Turing kernels for the problems of finding long simple paths and cycles in restricted graph families such as planar graphs, bounded-degree graphs, and claw-free graphs. The adaptive Turing kernelization works on the Tutte decomposition of the graph into triconnected components. Existing graph-theoretical lower bounds on the length of long paths in triconnected graphs allow us to answer YES if the Tutte decomposition has a bag of size superpolynomial in k. If this is not the case, we can identify a vertex that is irrelevant to the solution in polynomial time by querying an oracle for long paths or cycles in leaf components of the decomposition. The number of vertices involved in these queries is therefore polynomial in k, resulting in polynomial-size Turing kernels. The employed method is called Decompose-Query-Reduce and is potentially useful for other problems. Our Turing kernel shows that on these restricted graph classes, the hard part of the computation for finding a length-k path or cycle can be restricted to graphs whose size is polynomial in k.
27. Turing Kernelization for Finding Long Paths
and Cycles in Restricted Graph Classes
April 17th 2014, Chennai, India
In this informal board talk we present a set of new results concerning the existence of polynomial-size Turing kernels for the problems of finding long simple paths and cycles in restricted graph families such as planar graphs, bounded-degree graphs, and claw-free graphs. The adaptive Turing kernelization works on the Tutte decomposition of the graph into triconnected components. By processing the Tutte decomposition from bottom to top and making repeated use of the existence of an oracle that decides small instances of an NP-complete problem, we are able to reduce the size of the graph to polynomial in k without changing the answer. The employed method is called Decompose-Query-Reduce and is potentially useful for other problems. Our Turing kernel shows that on these restricted graph classes, the hard part of the computation for finding a length-k path or cycle can be restricted to graphs whose size is polynomial in k.
26. New developments in Circuit Complexity:
From Circuit-SAT Algorithms to Circuit Lower Bounds
March 20th 2014, Finse, Norway
In 2010, Ryan Williams suggested a new route to proving circuit lower bounds. He showed that the existence of algorithms for testing the satisfiability of a Boolean circuit that run slightly faster than brute force, imply superpolynomial circuit lower bounds for languages in the class NEXP. One year later he proved that for the restricted class of constant-depth circuits with mod gates (ACC) such circuit satisfiability algorithms exist. By adapting his earlier arguments this led to a proof that NEXP does not have non-uniform ACC circuits of polynomial size. In this tutorial we present the main ideas behind the proof while highlighting the role of algorithms in this circuit complexity breakthrough.
25. A Near-Optimal Planarization Algorithm
February 13th 2014, Dagstuhl, Germany
The problem of testing whether a graph is planar has been studied for over half a century, and is known to be solvable in O(n) time using a myriad of different approaches and techniques. Robertson and Seymour established the existence of a cubic algorithm for the more general problem of deciding whether an n-vertex graph can be made planar by at most k vertex deletions, for every fixed k. Of the known algorithms for k-Vertex Planarization, the algorithm of Marx and Schlotter (WG 2007, Algorithmica 2012) running in time 2^{k^{O(k^3)}} n^2 achieves the best running time dependence on k. The algorithm of Kawarabayashi (FOCS 2009), running in time f(k)n for some f(k) >= 2^{k^{k^3}} that is not stated explicitly, achieves the best dependence on n.
We present an algorithm for k-Vertex Planarization with running time 2^O(k log k) n, significantly improving the running time dependence on k without compromising the linear dependence on n. Our main technical contribution is a novel scheme to reduce the treewidth of the input graph to O(k) in time 2^O(k log k) n. It combines new insights into the structure of graphs that become planar after contracting a matching, with a Baker-type subroutine that reduces the number of disjoint paths through planar parts of the graph that are not affected by the sought solution. To solve the reduced instances we formulate a dynamic programming algorithm for Weighted Vertex Planarization on graphs of treewidth w with running time 2^O(w log w) n, thereby improving over previous double-exponential algorithms.
While Kawarabayashi's planarization algorithm relies heavily on deep results from the graph minors project, our techniques are elementary and practically self-contained. We expect them to be applicable to related edge-deletion and contraction variants of planarization problems.
24. A Near-Optimal Planarization Algorithm
January 7th 2014, Portland, Oregon, USA
The k-Vertex Planarization problem asks whether a graph G can be made planar by deleting k vertices. We show that the problem can be solved in time 2^O(k log k) n, thereby improving on an earlier algorithm by Kawarabayashi (FOCS 2009) with running time O(2^k^O(k^3)) * n. While earlier planarization algorithms relied heavily on deep results from the graph minors project, our techniques are elementary and practically self-contained.
23. On Sparsification for Computing Treewidth
November 27th 2013, Berlin, Germany
Many optimization problems can be solved efficiently on graphs of bounded treewidth, if a tree decomposition is known. Unfortunately, computing a minimum-width tree decomposition of a graph is NP-hard and can therefore form a bottleneck in such approaches. In the past, it has been observed that the use of heuristic reduction rules speeds up the process of finding tree decompositions significantly. We analyze two aspects of preprocessing for computing treewidth decompositions theoretically, using the framework of parameterized complexity.
Our first result concerns the possibility of polynomial-time sparsification. We study whether an n-vertex instance (G,k) of Treewidth, asking whether the graph G has treewidth at most k, can efficiently be made sparse without changing its answer. By giving a special form of OR-cross-composition, we prove that this is not the case: if there is an e>0 and a polynomial-time algorithm that reduces n-vertex Treewidth instances to equivalent instances, of an arbitrary problem, with O(n^{2-e}) bits, then NP is in coNP/poly and the polynomial hierarchy collapses. Our sparsification lower bound has implications for structural parameterizations of Treewidth: parameterizations by measures that do not exceed the vertex count, cannot have kernels with O(k^{2-e}) bits for any e>0, unless NP is in coNP/poly. In particular, the lower bound shows that Treewidth parameterized by the size of a vertex cover does not have a kernel with O(k^{2-e}) bits (unless ..).
Our second result tightens the gap between the upper- and lower bounds for Treewidth parameterized vertex cover. We improve the O(k^3)-vertex kernel from Bodlaender et al. (STACS 2011) to a kernel with O(k^2) vertices, which can be encoded in O(k^3) bits. Our improved kernel is based on a novel form of treewidth-invariant set. We use the q-expansion lemma of Fomin et al.(STACS 2011) to find such sets efficiently in graphs whose vertex count is superquadratic in their vertex cover number.
22. On Sparsification for Computing Treewidth
September 20th 2013, Bergen, Norway
We study whether an n-vertex instance (G,k) of Treewidth, asking whether the graph G has treewidth at most k, can efficiently be made sparse without changing its answer. By giving a special form of OR-cross-composition, we prove that this is not the case: if there is an e>0 and a polynomial-time algorithm that reduces n-vertex Treewidth instances to equivalent instances, of an arbitrary problem, with O(n^{2-e}) bits, then NP is in coNP/poly and the polynomial hierarchy collapses.
Our sparsification lower bound has implications for structural parameterizations of Treewidth: parameterizations by measures that do not exceed the vertex count, cannot have kernels with O(k^{2-e}) bits for any e>0, unless NP is in coNP/poly. Motivated by the question of determining the optimal kernel size for Treewidth parameterized by vertex cover, we improve the O(k^3)-vertex kernel from Bodlaender et al. (STACS 2011) to a kernel with O(k^2) vertices. Our improved kernel is based on a novel form of treewidth-invariant set. We use the q-expansion lemma of Fomin et al.(STACS 2011) to find such sets efficiently in graphs whose vertex count is superquadratic in their vertex cover number.
21. On Sparsification for Computing Treewidth
September 4th 2013, Sophia Antipolis, France
We study whether an n-vertex instance (G,k) of Treewidth, asking whether the graph G has treewidth at most k, can efficiently be made sparse without changing its answer. By giving a special form of OR-cross-composition, we prove that this is not the case: if there is an e>0 and a polynomial-time algorithm that reduces n-vertex Treewidth instances to equivalent instances, of an arbitrary problem, with O(n^{2-e}) bits, then NP is in coNP/poly and the polynomial hierarchy collapses.
Our sparsification lower bound has implications for structural parameterizations of Treewidth: parameterizations by measures that do not exceed the vertex count, cannot have kernels with O(k^{2-e}) bits for any e>0, unless NP is in coNP/poly. Motivated by the question of determining the optimal kernel size for Treewidth parameterized by vertex cover, we improve the O(k^3)-vertex kernel from Bodlaender et al. (STACS 2011) to a kernel with O(k^2) vertices. Our improved kernel is based on a novel form of treewidth-invariant set. We use the q-expansion lemma of Fomin et al.(STACS 2011) to find such sets efficiently in graphs whose vertex count is superquadratic in their vertex cover number.
20. FPT is Characterized by Useful Obstruction Sets
June 21st 2013, Lübeck, Germany
Many graph problems were first shown to be fixed-parameter tractable using the results of Robertson and Seymour on graph minors. We show that the combination of finite, computable, obstruction sets and efficient order tests is not just one way of obtaining strongly uniform FPT algorithms, but that all of FPT may be captured in this way. Our new characterization of FPT has a strong connection to the theory of kernelization, as we prove that problems with polynomial kernels can be characterized by obstruction sets whose elements have polynomial size. Consequently we investigate the interplay between the sizes of problem kernels and the sizes of the elements of such obstruction sets, obtaining several examples of how results in one area yield new insights in the other. We show how exponential-size minor-minimal obstructions for pathwidth k form the crucial ingredient in a novel OR-cross-composition for k-Pathwidth, complementing the trivial AND-composition that is known for this problem. In the other direction, we show that OR-cross-compositions into a parameterized problem can be used to rule out the existence of efficiently generated quasi-orders on its instances that characterize the NO-instances by polynomial-size obstructions.
19. Kernel Bounds for Structural Parameterizations of Pathwidth
July 6th 2012, Helsinki, Finland
Assuming the AND-distillation conjecture, the Pathwidth problem of determining whether a given graph G has pathwidth at most k admits no polynomial kernelization with respect to k. The present work studies the existence of polynomial kernels for Pathwidth with respect to other, structural, parameters.
Our main result is that, unless NP is contained in coNP/poly, Pathwidth admits no polynomial kernelization even when parameterized by the vertex deletion distance to a clique, by giving a cross-composition from Cutwidth. The cross-composition works also for Treewidth, improving over previous lower bounds by the present authors. For Pathwidth, our result rules out polynomial kernels with respect to the distance to various classes of polynomial-time solvable inputs, like interval or cluster graphs.
This leads to the question whether there are nontrivial structural parameters for which Pathwidth does admit a polynomial kernelization. To answer this, we give a collection of graph reduction rules that are safe for Pathwidth. We analyze the success of these results and obtain polynomial kernelizations with respect to the following parameters: the size of a vertex cover of the graph, the vertex deletion distance to a graph where each connected component is a star, and the vertex deletion distance to a graph where each connected component has at most c vertices.
18. Preprocessing Graph Problems: When Does a Small Vertex Cover Help?
June 13th 2012, Dagstuhl, Germany
We prove a number of results around kernelization of problems parameterized by the vertex cover of a graph. We provide two simple general conditions characterizing problems admitting kernels of polynomial size. Our characterizations not only give generic explanations for the existence of many known polynomial kernels for problems like Odd Cycle Transversal, Chordal Deletion, Planarization, eta-Transversal, Long Path, Long Cycle, or H-packing, they also imply new polynomial kernels for problems like F-Minor-Free Deletion, which is to delete at most k vertices to obtain a graph with no minor from a fixed finite set F.
While our characterization captures many interesting problems, the kernelization complexity landscape of problems parameterized by vertex cover is much more involved. We demonstrate this by several results about induced subgraph and minor containment, which we find surprising. While it was known that testing for an induced complete subgraph has no polynomial kernel unless NP is in coNP/poly, we show that the problem of testing if a graph contains a given complete graph on t vertices as a minor admits a polynomial kernel. On the other hand, it was known that testing for a path on t vertices as a minor admits a polynomial kernel, but we show that testing for containment of an induced path on t vertices is unlikely to admit a polynomial kernel.
17. Preprocessing for Treewidth: A Combinatorial Analysis through Kernelization
October 28th 2011, Bergen, Norway
In an informal blackboard-talk I will describe some results of a recent paper at ICALP, where we studied whether efficient preprocessing schemes for the Treewidth problem can give provable bounds on the size of the processed instances using the framework of kernelization. Assuming the AND-distillation conjecture to hold, the standard parameterization of Treewidth does not have a kernel of polynomial size and thus instances (G, k) of the decision problem of Treewidth cannot be efficiently reduced to equivalent instances of size polynomial in k. We therefore consider different (structural) parameterizations of the Treewidth problem. We show that Treewidth has a kernel with O(l^3) vertices, with l the size of a vertex cover, and a kernel with O(l^4) vertices, with l the size of a feedback vertex set. I will try to share some insights into how the reduction rules were found, and their relationship to experimental work on preprocessing heuristics for treewidth. We also obtained various kernel lower-bounds. Treewidth parameterized by the vertex-deletion distance to a co-cluster graph and Weighted Treewidth parameterized by the size of a vertex cover do not have polynomial kernels unless NP \subseteq coNP/poly. Treewidth parameterized by the deletion distance to a cluster graph has no polynomial kernel unless the AND-distillation conjecture does not hold. If time permits I will show which properties of treewidth were exploited in the reductions that yield these lower-bounds.
16. Kernel Bounds for Path and Cycle Problems
September 8th 2011, Saarbrücken, Germany
Connectivity problems like k-Path and k-Disjoint Paths relate to many important milestones in parameterized complexity, namely the Graph Minors Project, color coding, and the recent development of techniques for obtaining kernelization lower bounds. This work explores the existence of polynomial kernels for various path and cycle problems, by considering nonstandard parameterizations. We show polynomial kernels when the parameters are a given vertex cover, a modulator to a cluster graph, or a (promised) max leaf number. We obtain lower bounds via cross-composition, e.g., for Hamiltonian Cycle and related problems when parameterized by a modulator to an outerplanar graph.
15. Kernelization for a Hierarchy of Structural Parameters
September 3rd 2011, Vienna, Austria
There are various reasons to study the kernelization complexity of non-standard parameterizations. Problems such as Chromatic Number are NP-complete for a constant value of the natural parameter, hence we should not hope to obtain kernels for this parameter. For other problems such as Long Path, the natural parameterization is fixed-parameter tractable but is known not to admit a polynomial kernel unless the polynomial hierarchy collapses. We may therefore guide the search for meaningful preprocessing rules for these problems by studying the existence of polynomial kernels for different parameterizations.
Another motivation is formed by the Vertex Cover problem. Its natural parameterization admits a small kernel, but there exist refined parameters (such as the feedback vertex number) which are structually smaller than the natural parameter, for which polynomial kernels still exist; hence we may obtain better preprocessing studying the properties of such refined parameters.
In this survey talk we discuss recent results on the kernelization complexity of structural parameterizations of these important graph problems. We consider a hierarchy of structural graph parameters, and try to pinpoint the best parameters for which polynomial kernels still exist.
14. Data Reduction for Graph Coloring Problems
August 22nd 2011, Oslo, Norway
This paper studies the kernelization complexity of graph coloring problems, with respect to certain structural parameterizations of the input instances. We are interested in how well polynomial-time data reduction can provably shrink instances of coloring problems, in terms of the chosen parameter. It is well known that deciding 3-colorability is already NP-complete, hence parameterizing by the requested number of colors is not fruitful. Instead, we pick up on a research thread initiated by Cai (DAM, 2003) who studied coloring problems parameterized by the modification distance of the input graph to a graph class on which coloring is polynomial-time solvable; for example parameterizing by the number k of vertex-deletions needed to make the graph chordal. We obtain various upper and lower bounds for kernels of such parameterizations of q-Coloring, complementing Cai's study of the time complexity with respect to these parameters.
13. Vertex Cover Kernelization Revisited: Upper and Lower Bounds for a Refined Parameter
March 10th 2011, Dortmund, Germany
Kernelization is a concept that enables the formal mathematical analysis of data reduction through the framework of parameterized complexity. The parameterized Vertex Cover problem, which asks whether a given undirected graph G has a vertex subset S of size k such that G - S is edgeless, has been a testbed for various kernelization techniques. One of the major results in this direction is that it is possible to preprocess an instance (G,k) of Vertex Cover in polynomial time to obtain an equivalent instance (G',k') such that |V(G')| <= 2k' and k' <= k. This means that we can effectively reduce the size of the graphs that we have to consider for Vertex Cover, to a size which only depends on the size of the set we are looking for. In this work we consider whether we can bound the size of instances of Vertex Cover in a measure which is smaller than the size k of the desired vertex cover. A feedback vertex of a graph G is a set S such that G - S is a forest. Since any edgeless graph is a forest, the size of a minimum-size feedback vertex set (FVS) is at most the size of a vertex cover. Hence the parameter "size of a minimum FVS" is structurally smaller than the parameter "size of a minimum Vertex Cover". We prove that an instance of the decision problem "does graph G have a vertex cover of size k" can be preprocessed in polynomial time to obtain an equivalent instance where the number of vertices in the resulting instance is bounded by a polynomial in the minimum size of a FVS of G. In sharp contrast, we give complexity-theoretic evidence that no such data reduction is possible in the variant where the vertices of the graph G are weighted and we are looking for a minimum-weight vertex cover.
12. Vertex Cover Kernelization for a Refined Parameter: Upper and Lower bounds
January 12th 2011, Utrecht, The Netherlands
Kernelization is a concept that enables the formal mathematical analysis of data reduction through the framework of parameterized complexity. The parameterized Vertex Cover problem, which asks whether a given undirected graph G has a vertex subset S of size k such that G - S is edgeless, has been a testbed for various kernelization techniques. One of the major results in this direction is that it is possible to preprocess an instance (G,k) of Vertex Cover in polynomial time to obtain an equivalent instance (G',k') such that |V(G')| <= 2k' and k' <= k. This means that we can effectively reduce the size of the graphs that we have to consider for Vertex Cover, to a size which only depends on the size of the set we are looking for. In this work we consider whether we can bound the size of instances of Vertex Cover in a measure which is smaller than the size k of the desired vertex cover. A feedback vertex of a graph G is a set S such that G - S is a forest. Since any edgeless graph is a forest, the size of a minimum-size feedback vertex set (FVS) is at most the size of a vertex cover. Hence the parameter "size of a minimum FVS" is structurally smaller than the parameter "size of a minimum Vertex Cover". We prove that an instance of the decision problem "does graph G have a vertex cover of size k" can be preprocessed in polynomial time to obtain an equivalent instance where the number of vertices in the resulting instance is bounded by a polynomial in the minimum size of a FVS of G. In sharp contrast, we give complexity-theoretic evidence that no such data reduction is possible in the variant where the vertices of the graph G are weighted and we are looking for a minimum-weight vertex cover.
11. Vertex Cover Kernelization for a Refined Parameter: Upper and Lower bounds
January 7th 2011, Bergen, Norway
Kernelization is a concept that enables the formal mathematical analysis of data reduction through the framework of parameterized complexity. The parameterized Vertex Cover problem, which asks whether a given undirected graph G has a vertex subset S of size k such that G - S is edgeless, has been a testbed for various kernelization techniques. One of the major results in this direction is that it is possible to preprocess an instance (G,k) of Vertex Cover in polynomial time to obtain an equivalent instance (G',k') such that |V(G')| <= 2k' and k' <= k. This means that we can effectively reduce the size of the graphs that we have to consider for Vertex Cover, to a size which only depends on the size of the set we are looking for. In this work we consider whether we can bound the size of instances of Vertex Cover in a measure which is smaller than the size k of the desired vertex cover. A feedback vertex of a graph G is a set S such that G - S is a forest. Since any edgeless graph is a forest, the size of a minimum-size feedback vertex set (FVS) is at most the size of a vertex cover. Hence the parameter "size of a minimum FVS" is structurally smaller than the parameter "size of a minimum Vertex Cover". We prove that an instance of the decision problem "does graph G have a vertex cover of size k" can be preprocessed in polynomial time to obtain an equivalent instance where the number of vertices in the resulting instance is bounded by a polynomial in the minimum size of a FVS of G. In sharp contrast, we give complexity-theoretic evidence that no such data reduction is possible in the variant where the vertices of the graph G are weighted and we are looking for a minimum-weight vertex cover.
10. Kernelization Lower Bounds: Review of existing techniques and the introduction of Cross-composition
November 10th 2010, Leiden, The Netherlands
This presentation focuses on super-polynomial lower bounds on kernel sizes. The first half of the talk treats the existing techniques for proving such lower bounds. We start by considering OR-compositions, which allow us to prove that k-Path does not admit a polynomial kernel unless the polynomial hierarchy collapses. We then show that the framework can be extended by using polynomial-parameter transformations, which leads to a kernel lower bound for Disjoint Cycles by using the intermediate problem Disjoint Factors. Without going into details we discuss several other applications of this framework to obtain lower bounds for Connected Vertex Cover, Small Universe Set Cover and Small Universe Hitting Set. In the second half of the talk we introduce the new technique of cross-composition. We discuss how cross-composition generalizes and extends the two existing techniques, and give an application of cross-composition by proving that the Clique problem parameterized by size of a vertex cover of the graph does not admit a polynomial kernel (unless ..).
9. Vertex Cover Kernelization for a Refined Parameter: Upper and Lower bounds
September 10th 2010, Utrecht, The Netherlands
Kernelization is a concept that enables the formal mathematical analysis of data reduction through the framework of parameterized complexity. The parameterized Vertex Cover problem, which asks whether a given undirected graph G has a vertex subset S of size k such that G - S is edgeless, has been a testbed for various kernelization techniques. One of the major results in this direction is that it is possible to preprocess an instance (G,k) of Vertex Cover in polynomial time to obtain an equivalent instance (G',k') such that |V(G')| <= 2k' and k' <= k. This means that we can effectively reduce the size of the graphs that we have to consider for Vertex Cover, to a size which only depends on the size of the set we are looking for. In this work we consider whether we can bound the size of instances of Vertex Cover in a measure which is smaller than the size k of the desired vertex cover. A feedback vertex of a graph G is a set S such that G - S is a forest. Since any edgeless graph is a forest, the size of a minimum-size feedback vertex set (FVS) is at most the size of a vertex cover. Hence the parameter "size of a minimum FVS" is structurally smaller than the parameter "size of a minimum Vertex Cover". We prove that an instance of the decision problem "does graph G have a vertex cover of size k" can be preprocessed in polynomial time to obtain an equivalent instance where the number of vertices in the resulting instance is bounded by a polynomial in the minimum size of a FVS of G. In sharp contrast, we give complexity-theoretic evidence that no such data reduction is possible in the variant where the vertices of the graph G are weighted and we are looking for a minimum-weight vertex cover.
8. Polynomial Kernels for Hard Problems on Disk Graphs
June 23rd 2010, Bergen, Norway

7. Polynomial Kernels for Hard Problems on Disk Graphs
June 10th 2010, Aachen, Germany
Kernelization is a powerful tool to obtain fixed-parameter tractable algorithms. Recent breakthroughs show that many graph problems admit small polynomial kernels when restricted to sparse graph classes such as planar graphs, bounded-genus graphs or H-minor-free graphs. We consider the intersection graphs of (unit) disks in the plane, which can be arbitrarily dense but do exhibit some geometric structure. We give the first kernelization results on these dense graph classes. Connected Vertex Cover has a kernel with 12k vertices on unit-disk graphs and with 3k2+6k vertices on disk graphs with arbitrary radii. Red-Blue Dominating Set parameterized by the size of the smallest color class has a linear-vertex kernel on planar graphs, a quadratic-vertex kernel on unit-disk graphs and a quartic-vertex kernel on disk graphs. Finally we prove that H-matching on unit-disk graphs has a linear-vertex kernel for every fixed graph H.
6. Kernelization for Maximum Leaf Spanning Tree with Positive Vertex Weights
May 27th 2010, Rome, Italy
In this paper we consider a natural generalization of the well-known Max Leaf Spanning Tree problem. In the generalized Weighted Max Leaf problem we get as input an undirected connected graph G=(V,E), a rational number k≥1 and a weight function w mapping from vertices to rational numbers ≥ 1, and are asked whether a spanning tree T for G exists such that the combined weight of the leaves of T is at least k. We show that it is possible to transform an instance (G,w,k) of Weighted Max Leaf in linear time into an equivalent instance (G',w',k') such that |V'| ≤ 5.5k' and k'≤k. In the context of fixed parameter complexity this means that Weighted Max Leaf admits a kernel with 5.5k vertices. The analysis of the kernel size is based on a new extremal result which shows that every graph G that excludes some simple substructures always contains a spanning tree with at least |V|/5.5 leaves.
5. Polynomial Kernels for Hard Problems on Disk Graphs
April 16th 2010, Utrecht, The Netherlands
Kernelization is a powerful tool to obtain fixed-parameter tractable algorithms. Recent breakthroughs show that many graph problems admit small polynomial kernels when restricted to sparse graph classes such as planar graphs, bounded-genus graphs or H-minor-free graphs. We consider the intersection graphs of (unit) disks in the plane, which can be arbitrarily dense but do exhibit some geometric structure. We give the first kernelization results on these dense graph classes. Connected Vertex Cover has a kernel with 12k vertices on unit-disk graphs and with 3k2+6k vertices on disk graphs with arbitrary radii. Red-Blue Dominating Set parameterized by the size of the smallest color class has a linear-vertex kernel on planar graphs, a quadratic-vertex kernel on unit-disk graphs and a quartic-vertex kernel on disk graphs. Finally we prove that H-matching on unit-disk graphs has a linear-vertex kernel for every fixed graph H.
4. Fixed Parameter Complexity of the Weighted Max Leaf Problem
July 3rd 2009, Utrecht, The Netherlands
In this paper we consider the fixed parameter complexity of the Weighted Max Leaf problem, where we get as input an undirected connected graph G = (V,E) with a weight function w: V -> N on the vertices and are asked whether a spanning tree for G exists such that the combined weight of the leaves of the tree is at least k. The fixed parameter complexity of this problem strongly depends on the weight range that is allowed. If we allow vertices to have a weight of zero (the range of the weight function is the non-negative integers) then this problem is hard for W[1] on general graphs. When we restrict the problem to specific graph classes, we can obtain linear size problem kernels for these non-negative weights. We show the existence of a kernel with 78k vertices on planar graphs, O(sqrt(g)k + g) vertices on graphs of oriented genus at most g, and with (1 + 4d)(1 + d/2)k vertices on graphs in which the degree of positive-weight vertices is bounded by d. If we require all vertex weights to be strictly positive integers, we can prove the existence of a problem kernel with 7.5k vertices on general graphs. For the correctness proofs of the problem kernels we develop some extremal graph theory about spanning trees with many leaves in bipartite graphs, and in graphs that do not have long paths of degree-2 vertices.
3. Fixed parameter tractability and kernelization for the Maximum Leaf Weight Spanning Tree problem
May 12th 2009, Maastricht, The Netherlands
The Maximum Leaf Spanning Tree asks for a connected graph G and integer k whether there exists a spanning tree for G with at least k leaves. Recall that a leaf in a tree is a vertex with degree 1. The subject of this talk is the generalization of this problem into the Maximum Leaf Weight Spanning Tree (MLWST) problem, in which we give each vertex a non-negative integer weight and ask if the graph has a spanning tree such that the combined weight of all the leaves is at least k. We consider the fixed parameter (in)tractability of this problem. We show that MLWST is hard for W[1] on general graphs. The problem is Fixed Parameter Tractable (FPT) when restricted to graphs of bounded genus, which will be shown by presenting a linear sized problem kernel for these classes of graphs. This means that for those classes of graphs we can always apply polynomial time data reduction to simplify the problem instance to an equivalent instance whose size does not depend on |G|, but only on k.
2. Fixed parameter tractability and kernelization for the White-Black Max-Leaf Spanning Tree problem
March 6th 2009, Utrecht, The Netherlands
In the classic Maximum Leaf Spanning Tree problem, the input consists of a graph and the goal is to find a spanning tree for that graph that maximizes the number of leaves. We consider a generalization of the problem where the input consists of a graph whose vertices are colored either black or white, and the goal is to maximize the number of black leaves in a spanning tree. The problem is analyzed using the toolbox of parameterized complexity. We obtain several positive and negative results in the form of W[1]-hardness proofs and kernelization upper bounds. It turns out that to obtain positive results, we must restrict ourselves to planar graphs.
1. Heuristics for Road Network Augmentation
July 3rd 2008, Eindhoven, The Netherlands
In the social studies, it is common practice to study the relationship between socio-economic factors in various populations. It is not unusual for one of these factors to be the accessibility of a certain location. For example, one might study the correlation between the number of deaths in a certain village caused by a heart attack, and the proximity of that village to the nearest hospital. In general, the accessibility of speci c facilities often play a role in such studies.
When a detailed roadmap of an area is known, this roadmap can be used to compute shortest paths in a network. The lengths of these shortest paths can be used as a measure for accessibility. But these approaches fail when the road structure of an area is not known. Since there are large parts of the world for which there are no detailed roadmaps - think of third world countries, for example - this poses a problem when performing a socio-economic study on such an area. One solution to this problem is to augment the network with extra roads that are hypothesized to exist, but of which no information is known. The goal of such a step is to ensure that the road network forms a connected graph, such that regular accessibility analysis can be performed. In this talk we present experimental results on the results of various heuristics for road network augmentation.